题目内容
证明四个角相等的四边形是矩形.
考点:矩形的判定
专题:证明题
分析:先画出图形,写出已知、求证,先求出四边形是平行四边形,再求出∠A=90°,根据矩形的判定推出即可.
解答:已知:四边形ABCD,
∠A=∠B=∠C=∠D,
求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=∠D,
∴∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,
∵∠A=∠B=∠C=∠D,∠A+∠B+∠C+∠D=360°,
∴∠A=90°,
∴四边形ABCD是矩形.

∠A=∠B=∠C=∠D,
求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=∠D,
∴∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,
∵∠A=∠B=∠C=∠D,∠A+∠B+∠C+∠D=360°,
∴∠A=90°,
∴四边形ABCD是矩形.
点评:本题考查了四边形内角和定理,平行四边形的判定,矩形的判定的应用,注意:有一个角是直角的平行四边形是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
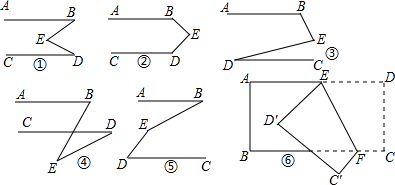
 如图,一个梯子AB长2.5m,顶端A靠在墙OB上,这时梯子下端A与墙角O距离为0.7m,梯子滑动后停在A′B′的位置上,测得BB′长为0.4m,求梯子底端A滑动了多少米.
如图,一个梯子AB长2.5m,顶端A靠在墙OB上,这时梯子下端A与墙角O距离为0.7m,梯子滑动后停在A′B′的位置上,测得BB′长为0.4m,求梯子底端A滑动了多少米.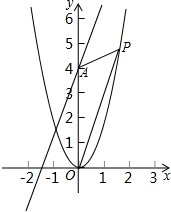 在平面直角坐标系中,O为坐标原点,直线y=3x+4交y轴于点A,在抛物线y=2x2上是否存在一点P,使△POA的面积等于10?若存在,求出P点坐标;若不存在,说明理由.
在平面直角坐标系中,O为坐标原点,直线y=3x+4交y轴于点A,在抛物线y=2x2上是否存在一点P,使△POA的面积等于10?若存在,求出P点坐标;若不存在,说明理由.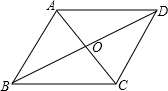 已知:如图,菱形ABCD的边长为4,∠ABC=60°,对角线AC和BD相交于点O,求AC,BD的长和菱形的面积.
已知:如图,菱形ABCD的边长为4,∠ABC=60°,对角线AC和BD相交于点O,求AC,BD的长和菱形的面积.