题目内容
直线y=kx+b经过A(2,1)、B(-1,-2)两点,求不等式
x>kx+b的解集.
| 1 |
| 2 |
考点:一次函数与一元一次不等式
专题:计算题
分析:先把A点和B点坐标代入y=kx+b得到关于k、b的方程组,再解方程组得到k、b的值,然后解不等式
x>x-1即可.
| 1 |
| 2 |
解答:解:把A(2,1)、B(-1,-2)代入y=kx+b得
,解得
,
即直线解析式为y=x-1,
解不等式
x>x-1得x<2,
即不等式
x>kx+b的解集为x<2.
|
|
即直线解析式为y=x-1,
解不等式
| 1 |
| 2 |
即不等式
| 1 |
| 2 |
点评:本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
观察下列各式:0.
=
,0.
=
,0.
=
,又如0.
=
,0.52
=
,0.1
=
,0.35
=
,则把0.173
化成分数是( )
| • |
| 2 |
| 2 |
| 9 |
| •• |
| 23 |
| 23 |
| 99 |
| … |
| 153 |
| 153 |
| 999 |
| •• |
| 23 |
| 23-2 |
| 90 |
| • |
| 7 |
| 527-52 |
| 900 |
| •• |
| 26 |
| 126-1 |
| 990 |
| •• |
| 42 |
| 3542-35 |
| 9900 |
| •• |
| 29 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知AD∥BC,∠BAD=∠BCD,AE平分∠BAD,CF平分∠BCD,求证:AE∥FC.
如图,已知AD∥BC,∠BAD=∠BCD,AE平分∠BAD,CF平分∠BCD,求证:AE∥FC. 已知,如图,点A,B,C分别在△EFD的各边上,且AB∥DE,BC∥EF,CA∥FD,求证:A,B,C分别是△EFD各边的中点.
已知,如图,点A,B,C分别在△EFD的各边上,且AB∥DE,BC∥EF,CA∥FD,求证:A,B,C分别是△EFD各边的中点. 已知:如图,∠1=∠2,∠C=∠D,请由此找出所有互相平行的直线,并说明理由.
已知:如图,∠1=∠2,∠C=∠D,请由此找出所有互相平行的直线,并说明理由.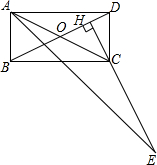 如图,在矩形ABCD中,点H在对角线BD上.HC⊥BD,HC的延长线交∠BAD的平分线于点E.求证:CE=BD.
如图,在矩形ABCD中,点H在对角线BD上.HC⊥BD,HC的延长线交∠BAD的平分线于点E.求证:CE=BD.