题目内容
 如图,已知四边形ABCD是中心对称图形,E、F是对角线BD上的两点,且DE=BF,求证:
如图,已知四边形ABCD是中心对称图形,E、F是对角线BD上的两点,且DE=BF,求证:(1)△ADE≌△CBF;
(2)AE∥CF.
考点:中心对称,全等三角形的判定与性质
专题:证明题
分析:(1)根据中心对称的性质可得AD=BC,∠ADE=∠CBF,然后利用“边角边”证明△ADE和△CBF全等即可;
(2)根据全等三角形对应角相等可得∠AED=∠CFB,再根据等角的补角相等求出∠AEF=∠CFE,然后根据内错角相等,两直线平行证明.
(2)根据全等三角形对应角相等可得∠AED=∠CFB,再根据等角的补角相等求出∠AEF=∠CFE,然后根据内错角相等,两直线平行证明.
解答:证明:(1)∵四边形ABCD是中心对称图形,
∴AD=BC,∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)∵△ADE≌△CBF,
∴∠AED=∠CFB,
∴180°-∠AED=180°-∠CFB,
即∠AEF=∠CFE,
∴AE∥CF.
∴AD=BC,∠ADE=∠CBF,
在△ADE和△CBF中,
|
∴△ADE≌△CBF(SAS);
(2)∵△ADE≌△CBF,
∴∠AED=∠CFB,
∴180°-∠AED=180°-∠CFB,
即∠AEF=∠CFE,
∴AE∥CF.
点评:本题考查了中心对称的性质,全等三角形的判定与性质,熟练掌握中心对称的性质得到相等的边和角从而得到三角形全等的条件是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
a、b、c是三角形的三条边长,则代数式a2-2ab+b2-c2的值( )
| A、大于零 | B、小于零 |
| C、等于零 | D、与零的大小无关 |
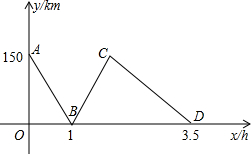 如图,甲、丙两地相距500km,一列快车从甲地驶往丙地且途中经过乙地,一列慢车从乙地驶往丙地,两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究.
如图,甲、丙两地相距500km,一列快车从甲地驶往丙地且途中经过乙地,一列慢车从乙地驶往丙地,两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究.