题目内容
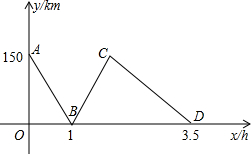 如图,甲、丙两地相距500km,一列快车从甲地驶往丙地且途中经过乙地,一列慢车从乙地驶往丙地,两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究.
如图,甲、丙两地相距500km,一列快车从甲地驶往丙地且途中经过乙地,一列慢车从乙地驶往丙地,两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究.(1)甲乙两地之间的距离为多少?
(2)求慢车和快车的速度;
(3)求线段CD所表示的y与x的函数关系式,并写出自变量x的取值范围.
考点:一次函数的应用
专题:
分析:(1)因为两车同时出发,同向而行,所以A点就是甲乙两地之间的距离为150千米;
(2)图中B点为y=0,即快慢两车的距离为0,所以B点表示快慢两车相遇的时间.由A点为两车的路程差,相遇时间为1小时,可知:快车速度-慢车速度=150,再由点D可知慢车3.5小时从乙地到达丙地;由此求出慢车速度,进一步求出快车速度;
(3)C点表示就是当快车到达丙地时,慢车快车的距离即慢车与丙地的距离,由路程除以速度算出慢车到达丙地的时间(就是C点的纵坐标),以及慢车距离丙地的距离(就是C点的纵坐标),得出
点C坐标,设出函数解析式,代入求得即可根据坐标求得自变量的取值范围.
(2)图中B点为y=0,即快慢两车的距离为0,所以B点表示快慢两车相遇的时间.由A点为两车的路程差,相遇时间为1小时,可知:快车速度-慢车速度=150,再由点D可知慢车3.5小时从乙地到达丙地;由此求出慢车速度,进一步求出快车速度;
(3)C点表示就是当快车到达丙地时,慢车快车的距离即慢车与丙地的距离,由路程除以速度算出慢车到达丙地的时间(就是C点的纵坐标),以及慢车距离丙地的距离(就是C点的纵坐标),得出
点C坐标,设出函数解析式,代入求得即可根据坐标求得自变量的取值范围.
解答:解:(1)∵点A(0,150),
∴甲乙两地之间的距离为150km;
(2)慢车速度:(500-150)÷3.5=100km/h;
快车速度:150+100=250km/h;
(3)500÷250=2h,
350-100×2=150km,
∴点C坐标为(2,150),
设yCD=kx+b,
把点C(2,150),D(3.5,0)代入得
解得
∴yCD=-100x+350(2≤x≤3.5).
∴甲乙两地之间的距离为150km;
(2)慢车速度:(500-150)÷3.5=100km/h;
快车速度:150+100=250km/h;
(3)500÷250=2h,
350-100×2=150km,
∴点C坐标为(2,150),
设yCD=kx+b,
把点C(2,150),D(3.5,0)代入得
|
解得
|
∴yCD=-100x+350(2≤x≤3.5).
点评:此题考查一次函数的综合运用,解答问题的关键是看清图象表示的意义,利用路程、时间、速度三者之间的关系解决问题.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E是AB的中点,图中与△ADE面积相等(△ADE除外)的三角形有( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E是AB的中点,图中与△ADE面积相等(△ADE除外)的三角形有( )| A、1个 | B、3个 | C、5个 | D、6个 |
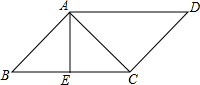 如图,在平行四边形ABCD中,已知AC⊥CD,AE⊥BC,若∠EAC=50°,求∠D的度数.
如图,在平行四边形ABCD中,已知AC⊥CD,AE⊥BC,若∠EAC=50°,求∠D的度数. 如图,已知四边形ABCD是中心对称图形,E、F是对角线BD上的两点,且DE=BF,求证:
如图,已知四边形ABCD是中心对称图形,E、F是对角线BD上的两点,且DE=BF,求证: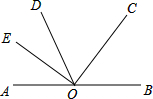 如图,O为直线AB上一点,OC平分∠BOD,OE⊥OC,垂足为O,∠AOE与∠DOE有什么关系,请说明理由.
如图,O为直线AB上一点,OC平分∠BOD,OE⊥OC,垂足为O,∠AOE与∠DOE有什么关系,请说明理由.