题目内容
5. 如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=3.
如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=3.
分析 连接CD,BD,由∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,根据角平分线的性质与线段垂直平分线的性质,易得CD=BD,DF=DE,继而可得AF=AE,易证得Rt△CDF≌Rt△BDE,则可得BE=CF,继而求得答案.
解答 解:如图,连接CD,BD,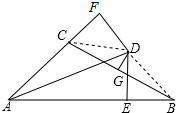
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,
∴AE=AF,
∵DG是BC的垂直平分线,
∴CD=BD,
在Rt△CDF和Rt△BDE中,
$\left\{\begin{array}{l}{CD=BD}\\{DF=DE}\end{array}\right.$,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
∵AB=11,AC=5,
∴BE=$\frac{1}{2}$(11-5)=3.
故答案为:3.
点评 此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
18.下列四个式子中,是一元一次方程的为( )
| A. | $\frac{1}{x}-2=x$ | B. | y=2-3y | C. | x2=2x | D. | x+2=3y |
1.若a-b+c=0,a≠0,则方程ax2+bx+c=0必有一个根是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 不能确定 |
17.正三角形的高、外接圆半径、边心距之比为( )
| A. | 1:2:2$\sqrt{3}$ | B. | 1:2:$\sqrt{3}$ | C. | 3:2:1 | D. | 1:2:3 |
 已知三角形的三个顶点都在表格的交点上,其中A(3,3),B(3,5),请在表格中确定C点的位置,使S△ABC=1,这样的点C有多少个,请分别表示出来.
已知三角形的三个顶点都在表格的交点上,其中A(3,3),B(3,5),请在表格中确定C点的位置,使S△ABC=1,这样的点C有多少个,请分别表示出来. 如图,Rt△ABC中,∠C=90°,BC=4,AC=8,⊙O与边BC相切于点B,且经过点A,则⊙O的半径为5.
如图,Rt△ABC中,∠C=90°,BC=4,AC=8,⊙O与边BC相切于点B,且经过点A,则⊙O的半径为5.