题目内容
17.正三角形的高、外接圆半径、边心距之比为( )| A. | 1:2:2$\sqrt{3}$ | B. | 1:2:$\sqrt{3}$ | C. | 3:2:1 | D. | 1:2:3 |
分析 连接OB,AO,延长AO交BC于D,根据⊙O是等边三角形ABC的外接圆求出∠OBC=30°,推出OB=2OD,求出AD=$\frac{3}{2}$OB,代入求出即可.
解答 解:连接OB,AO,延长AO交BC于D,
设正三角形的边长为a,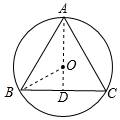
∵⊙O是等边三角形ABC的外接圆,
∴AD⊥BC,∠OBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,
∴BD=$\frac{1}{2}$a.
∵∠ADB=90°,∠OBC=30°,
∴OD=BD×tan30°=$\frac{\sqrt{3}}{6}$,OB=$\frac{\sqrt{3}}{3}$a,AD=AB•cos30°=$\frac{\sqrt{3}}{2}$a,
∴正三角形的高、外接圆半径、边心距之比=AD:OB:OD═3:2:1.,
故选:C.
点评 本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
9.如果把分式$\frac{xy}{x+y}$中的x和y都扩大3倍,那么分式的值( )
| A. | 扩大3倍 | B. | 扩大9倍 | C. | 扩大4倍 | D. | 不变 |
12.某商人一次卖出两件衣服,一件赚了百分之15,一件亏了百分之15,售价都是9775元,在这次生意中,该商人( )
| A. | 不赚不赔 | B. | 赚了490元 | C. | 亏了450元 | D. | 亏了490元 |
9.关于函数y=-2x+1,下列结论正确的是( )
| A. | 图象必经过点(-2,1) | B. | y随x的增大而增大 | ||
| C. | 当x>$\frac{1}{2}$时,y<0 | D. | 图象不经过第一象限 |
 如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=3.
如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=3.