题目内容
15．已知k＞0，b＜0，则直线y=kx-b的大致图象是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 直接根据一次函数的图象与系数的关系即可得出结论．
解答 解：∵k＞0，b＜0，
∴-b＞0，
∴直线y=kx-b经过第一二三象限．
故选B．
点评 本题考查的是一次函数的图象与系数的关系，熟知一次函数y=kx+b（k≠0）中，当k＞0，b＞0时，函数图象经过第一二三象限是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．有这样一个问题：探究函数y=x-1+$\frac{1}{x-2}$的图象与性质．
下面是小东的探究过程，请补充完成：
（1）函数y=x-1+$\frac{1}{x-2}$的自变量x的取值范围是x≠2．
（2）在平面直角坐标系xOy中描出了图象上的一些点，请你画出函数的图象；
下表是y与x的几组对应值．
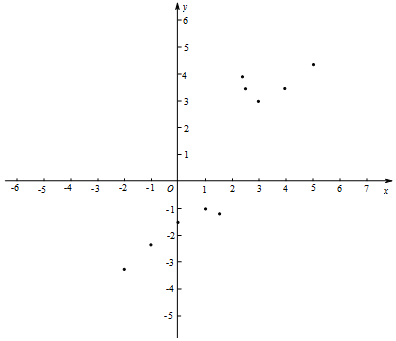
（3）求m的值；
（4）根据图象写出此函数的一条性质．
下面是小东的探究过程，请补充完成：
（1）函数y=x-1+$\frac{1}{x-2}$的自变量x的取值范围是x≠2．
（2）在平面直角坐标系xOy中描出了图象上的一些点，请你画出函数的图象；
下表是y与x的几组对应值．
| x | … | -2 | -1 | 0 | 1 | 1.4 | 2.4 | 2.5 | 3 | 4 | 5 | … |
| y | … | -3.25 | -2.33 | -1.50 | -1 | -1.27 | 3.9 | 3.5 | 3 | m | 4.33 | … |
（3）求m的值；
（4）根据图象写出此函数的一条性质．
6．为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水，对居民家庭每户每月用水量采用分档递增收费的方式，每户每月用水量不超过基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费．为对基本用水量进行决策，随机抽查2000户居民家庭每户每月用水量的数据，整理绘制出下面的统计表：
（1）为确保70%的居民家庭每户每月的基本用水量需求，那么每户每月的基本用水量最低应确定为多少立方米？
（2）若将（1）中确定的基本用水量及其以内的部分按每立方米1.8元交费，超过基本用水量的部分按每立方米2.5元交费．设x表示每户每月用水量（单位：m3），y表示每户每月应交水费（单位：元），求y与x的函数关系式；
（3）某户家庭每月交水费是80.9元，请按以上收费方式计算该家庭当月用水量是多少立方米？
| 用户每月用水量（m3） | 32及其以下 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43及其以上 |
| 户数（户） | 200 | 160 | 180 | 220 | 240 | 210 | 190 | 100 | 170 | 120 | 100 | 110 |
（2）若将（1）中确定的基本用水量及其以内的部分按每立方米1.8元交费，超过基本用水量的部分按每立方米2.5元交费．设x表示每户每月用水量（单位：m3），y表示每户每月应交水费（单位：元），求y与x的函数关系式；
（3）某户家庭每月交水费是80.9元，请按以上收费方式计算该家庭当月用水量是多少立方米？
3．已知某种细菌的直径为0.0000302mm，用科学记数法表示为（ ）
| A． | 3.02×10-5mm | B． | 30.2×10-6mm | C． | 302×10-4mm | D． | 302×10-8mm |
10．下列命题中，是真命题的是（ ）
| A． | 相等的角是对顶角 | |
| B． | 和为180°的两个角是邻补角 | |
| C． | 两条直线被第三条直线所截，同位角相等 | |
| D． | 过直线外一点，有且只有一条直线与已知直线平行 |
7．植树节这天，35名同学共栽了90棵树苗，其中男生每人栽3棵，女生每人栽2棵．若设男生有x人，女生有y人，则下列方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=35}\\{2x+3y=90}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=35}\\{3x+2y=90}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+y=90}\\{2x+3y=35}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=90}\\{3x+2y=35}\end{array}\right.$ |
4．若|x2-4x+4|与$\sqrt{2x-y-3}$互为相反数，则x+y的值为（ ）
| A． | 3 | B． | 4 | C． | 6 | D． | 9 |
