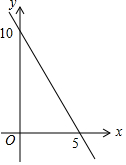题目内容
4．若|x2-4x+4|与$\sqrt{2x-y-3}$互为相反数，则x+y的值为（ ）| A． | 3 | B． | 4 | C． | 6 | D． | 9 |
分析 根据相反数的定义得到|x2-4x+4|+$\sqrt{2x-y-3}$=0，再根据非负数的性质得x2-4x+4=0，2x-y-3=0，然后利用配方法求出x，再求出y，最后计算它们的和即可．
解答 解：根据题意得|x2-4x+4|+$\sqrt{2x-y-3}$=0，
所以|x2-4x+4|=0，$\sqrt{2x-y-3}$=0，
即（x-2）2=0，2x-y-3=0，
所以x=2，y=1，
所以x+y=3．
故选A．
点评 本题考查了解一元二次方程-配方法：将一元二次方程配成（x+m）2=n的形式，再利用直接开平方法求解，这种解一元二次方程的方法叫配方法．也考查了非负数的性质．
练习册系列答案
教材全解字词句篇系列答案
相关题目
14．为配合荆州市“我读书，我快乐”读书节活动，某书店推出一种优惠卡，每张卡售价20元，凭卡购书可享受8折优惠．小慧同学到该书店购书，她先买优惠卡再凭卡付款，结果节省了10元．若此次小慧同学不买卡直接购书，则她需付款多少元？（ ）
| A． | 140元 | B． | 150元 | C． | 160元 | D． | 200元 |
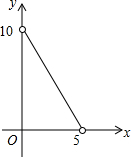
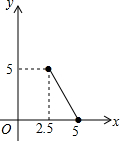
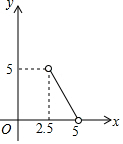
15．已知k＞0，b＜0，则直线y=kx-b的大致图象是（ ）
| A． |  | B． |  | C． |  | D． |  |
19．
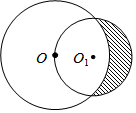如图，一个半径为1的⊙O1经过一个半径为$\sqrt{2}$的⊙O的圆心，则图中阴影部分的面积为（ ）
如图，一个半径为1的⊙O1经过一个半径为$\sqrt{2}$的⊙O的圆心，则图中阴影部分的面积为（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | $\sqrt{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
