题目内容
 如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上,DF平分∠BDE,DF与BC交于点F.
如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上,DF平分∠BDE,DF与BC交于点F.(1)依题意补全图形;
(2)若∠B+∠BDF=90°,求证:∠A=∠EDF.
证明:∵∠A+∠B=90°,∠B+∠BDF=90°
∴
又∵
∴∠BDF=∠EDF(理由:
∴∠A=∠EDF.
考点:余角和补角,角平分线的定义
专题:推理填空题
分析:(1)画出DF平分∠BDE;
(2)首先根据∠A+∠B=90°,∠B+∠BDF=90°可得∠A=∠BDF,再根据DF平分∠BDE可得∠BDF=∠EDF,进而可得∠A=∠EDF.
(2)首先根据∠A+∠B=90°,∠B+∠BDF=90°可得∠A=∠BDF,再根据DF平分∠BDE可得∠BDF=∠EDF,进而可得∠A=∠EDF.
解答: (1)解:如图所示:
(1)解:如图所示:
(2)证明:∵∠A+∠B=90°,∠B+∠BDF=90°
∴∠A=∠BDF(同角的余角相等),
又∵DF平分∠BDE,
∴∠BDF=∠EDF(角平分线定义),
∴∠A=∠EDF.
 (1)解:如图所示:
(1)解:如图所示:(2)证明:∵∠A+∠B=90°,∠B+∠BDF=90°
∴∠A=∠BDF(同角的余角相等),
又∵DF平分∠BDE,
∴∠BDF=∠EDF(角平分线定义),
∴∠A=∠EDF.
点评:此题主要考查了角平分线的性质,以及余角的性质,关键是掌握等角的补角相等.等角的余角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 实数a、b在数轴上的位置如图所示,且|a|<|b|,则化简|a+b|-
实数a、b在数轴上的位置如图所示,且|a|<|b|,则化简|a+b|-| a2 |
| A、b | B、-2a+b |
| C、-2a-b | D、2a+b |
在Rt△ABC中,∠C=90°,若AB=
,BC=2,则sinB的值为( )
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,将一个直角三角形板AOB的顶点O放在直线CD上,若∠AOC=35°,则∠BOD等于( )
如图,将一个直角三角形板AOB的顶点O放在直线CD上,若∠AOC=35°,则∠BOD等于( )| A、155° | B、145° |
| C、65° | D、55° |
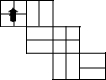
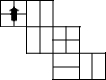
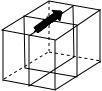 小明制作了一个正方体包装盒,他在这个正方体包装盒的上面设计了一个“
小明制作了一个正方体包装盒,他在这个正方体包装盒的上面设计了一个“ ”标志,并在正方体的每个表面都画了黑色粗线,如图所示在下列图形中,是这个正方体包装盒的表面展开图的是( )
”标志,并在正方体的每个表面都画了黑色粗线,如图所示在下列图形中,是这个正方体包装盒的表面展开图的是( )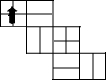

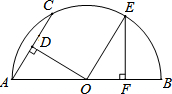 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( ) 在Rt△ABC中,∠C=90°,∠BDC=45°,BC=1,DA=
在Rt△ABC中,∠C=90°,∠BDC=45°,BC=1,DA=