题目内容
在Rt△ABC中，∠C=90°，∠BDC=45°，BC=1，DA=| 3 |
考点：勾股定理,等腰直角三角形
专题：
分析：根据等腰直角三角形的性质可得CD=BC=1，根据AC=AD+CD可求AC，再根据勾股定理即可求得AB的长．
解答：解：∵∠C=90°，∠BDC=45°，
∴△BCD是等腰直角三角形，
∴CD=BC=1，
∵DA=
-1，
∴AC=
，
在Rt△ABC中，AB=
=2．
故AB的长是2．
∴△BCD是等腰直角三角形，
∴CD=BC=1，
∵DA=
| 3 |
∴AC=
| 3 |
在Rt△ABC中，AB=
| AC2+BC2 |
故AB的长是2．
点评：本题主要考查勾股定理的知识，涉及了等腰直角三角形的性质，关键在于推出CD和AC的长度．
练习册系列答案
名校课堂系列答案
相关题目
如图，∠AOC与∠BOD是对顶角，OE平分∠AOC，OF平分∠BOD，求∠EOF的度数．
如图，∠A+∠B=90°，点D在线段AB上，点E在线段AC上，DF平分∠BDE，DF与BC交于点F．
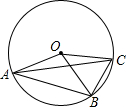如图，OA，OB，OC都是⊙O的半径，若∠AOB是锐角，且∠AOB=2∠BOC．则下列结论正确的是（ ）| A、AB=2BC |
| B、AB＜2BC |
| C、∠AOB=2∠CAB |
| D、∠ACB=4∠CAB |
若一个三角形不在同一顶点的两个外角的和为300°，那么这个三角形是（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、以上都可能 |