题目内容
 实数a、b在数轴上的位置如图所示,且|a|<|b|,则化简|a+b|-
实数a、b在数轴上的位置如图所示,且|a|<|b|,则化简|a+b|-| a2 |
| A、b | B、-2a+b |
| C、-2a-b | D、2a+b |
考点:实数与数轴
专题:
分析:由数轴得出b<0<a,又|a|<|b|,所以原式化简为|a+b|-a,去掉绝对值符号得出-a-b-a,合并同类项即可.
解答:解:∵由数轴可知:b<0<a,|a|<|b|,
∴|a+b|-
=|a+b|-a
=-a-b-a
=-2a-b.
故选C.
∴|a+b|-
| a2 |
=|a+b|-a
=-a-b-a
=-2a-b.
故选C.
点评:本题考查了二次根式的性质与化简和实数与数轴的应用,解此题的关键是根据数轴得出b<0<a,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
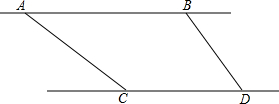
 如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,则∠EBA的度数为
如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,则∠EBA的度数为



 如图,∠AOC与∠BOD是对顶角,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数.
如图,∠AOC与∠BOD是对顶角,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数. 如图所示,AC是∠BAD的平分线,CE是∠ACD的平分线,那么图中相等的角有几对?分别是哪些角?
如图所示,AC是∠BAD的平分线,CE是∠ACD的平分线,那么图中相等的角有几对?分别是哪些角?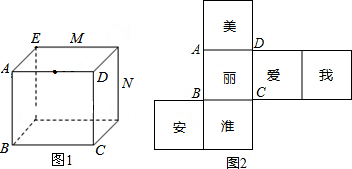
 2014年3月8日凌晨,马来西亚航空公司MH370航班与总部失去联系,我国随即针对该航班展开了大规模搜救行动,我国的侦察机和搜救船在某海域同时沿同一方向配合搜寻(如图13).在距海面900米的高空A处,侦察机测得搜救船在俯角为30°的海面C处,当侦察机以150
2014年3月8日凌晨,马来西亚航空公司MH370航班与总部失去联系,我国随即针对该航班展开了大规模搜救行动,我国的侦察机和搜救船在某海域同时沿同一方向配合搜寻(如图13).在距海面900米的高空A处,侦察机测得搜救船在俯角为30°的海面C处,当侦察机以150 如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上,DF平分∠BDE,DF与BC交于点F.
如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上,DF平分∠BDE,DF与BC交于点F.