题目内容
1．成都市为了解决街道路面问题，需在中心城区重新铺设一条长3000米的路面，实施施工时“…”，设实际每天铺设路面x米，则可得方程$\frac{3000}{x-10}$-$\frac{3000}{x}$=15，根据此情景，题中用“…”表示的缺失的条件应补为（ ）| A． | 每天比原计划多铺设10米，结果延期15天才完成 | |
| B． | 每天比原计划少铺设10米，结果延期15天才完成 | |
| C． | 每天比原计划多铺设10米，结果提前15天才完成 | |
| D． | 每天比原计划少铺设10米，结果提前15天才完成 |
分析 根据工作时间=工作总量÷工作效率，得出3000÷x表示实际的工作时间，那么3000÷（x-10）就表示原计划的工作时间，15就代表现在比原计划少的时间，从而得出正确答案．
解答 解：设实际每天铺设管道x米，原计划每天铺设管道（x-10）米，方程$\frac{3000}{x-10}$-$\frac{3000}{x}$=15，则表示实际用的时间-原计划用的时间=15天，
那么就说明实际每天比原计划多铺设10米，结果提前15天完成任务．
故选C．
点评 本题主要考查了由实际问题抽象出分式方程，根据方程来判断缺失的条件，要注意方程所表示的意思，结合题目给出的条件得出正确的判断．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
12．若a＞b，则下列不等式中正确的是（ ）
| A． | a-1＞b-1 | B． | a-b＜0 | C． | $\frac{a}{2}$＜$\frac{b}{2}$ | D． | -3a＞-3b |
13．下列各组中，不是二元一次方程x+2y=5的解的是（ ）
| A． | $\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$ | B． | $\left\{\begin{array}{l}x=2\\ y=1.5\end{array}\right.$ | C． | $\left\{\begin{array}{l}x=6\\ y=-1\end{array}\right.$ | D． | $\left\{\begin{array}{l}x=9\\ y=-2\end{array}\right.$ |
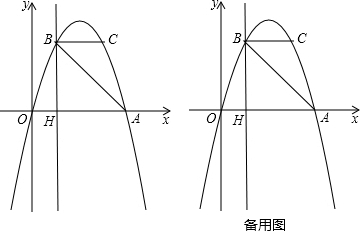
如图，四边形ABCD中，AC、BD交于O点且AC⊥BD，AB、CD所在的直线为l1、l2，l1∥l2．若AC=8，BD=6，固定线段AC不动，线段BD在l1、l2之间平移．