题目内容
6.三元一次方程组$\left\{\begin{array}{l}x+2y=5\\ 2y+z=1\\ x+z=10.\end{array}\right.$的解是$\left\{\begin{array}{l}{x=7}\\{y=-1}\\{z=3}\end{array}\right.$.分析 先由③-②得出x-2y=9④,①④联立得到方程组$\left\{\begin{array}{l}{x+2y=5}\\{x-2y=9}\end{array}\right.$,解方程组得到x,y的值,进一步即可求解.
解答 解:$\left\{\begin{array}{l}{x+2y=5①}\\{2y+z=1②}\\{x+z=10③}\end{array}\right.$,
③-②得x-2y=9④,
①④联立得到方程组$\left\{\begin{array}{l}{x+2y=5}\\{x-2y=9}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=7}\\{y=-1}\end{array}\right.$,
把x=7代入③得7+z=10,
解得z=3.
故原方程组的解为$\left\{\begin{array}{l}{x=7}\\{y=-1}\\{z=3}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=7}\\{y=-1}\\{z=3}\end{array}\right.$.
点评 本题考查了三元一次方程组的解法,三元一次方程组的解法是把“三元”转化为“二元”、把“二元”转化为“一元”,解题之前先观察方程组中的方程的系数特点,认准易消的未知数,要注意加减法的灵活应用.

练习册系列答案
相关题目
16.某县政府2013年投资0.5亿元用于保障性住房建设,计划到2015年投资保障性住房建设的资金为0.98亿元,如果从2013年到2015年投资此项目资金的年增长率相同,那么年增长率是( )
| A. | 30% | B. | 40% | C. | 50% | D. | 10% |
17.分式方程$\frac{2}{x-3}$=$\frac{3}{x}$的解为( )
| A. | x=0 | B. | x=5 | C. | x=3 | D. | x=9 |
14.若a与2013互为相反数,则a的倒数为( )
| A. | -2013 | B. | 2013 | C. | $\frac{1}{2013}$ | D. | $-\frac{1}{2013}$ |
1.成都市为了解决街道路面问题,需在中心城区重新铺设一条长3000米的路面,实施施工时“…”,设实际每天铺设路面x米,则可得方程$\frac{3000}{x-10}$-$\frac{3000}{x}$=15,根据此情景,题中用“…”表示的缺失的条件应补为( )
| A. | 每天比原计划多铺设10米,结果延期15天才完成 | |
| B. | 每天比原计划少铺设10米,结果延期15天才完成 | |
| C. | 每天比原计划多铺设10米,结果提前15天才完成 | |
| D. | 每天比原计划少铺设10米,结果提前15天才完成 |
11.下列式子中,是一元一次方程的是( )
| A. | 3x+1=4x | B. | x+2>1 | C. | x2-9=0 | D. | 2x-3y=0 |
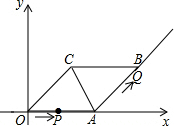 已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从O点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从O点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.