题目内容
2.当|k-2b|+$\sqrt{k+b-3}$=0时,直线y=kx+b经过点( )| A. | (-1,-1) | B. | (-1,1) | C. | (-1,-3) | D. | (-1,3) |
分析 根据非负性得出k与b的值解答即可.
解答 解:因为|k-2b|+$\sqrt{k+b-3}$=0,
可得:$\left\{\begin{array}{l}{k-2b=0}\\{k+b-3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=1}\end{array}\right.$,
所以直线y=kx+b的解析式为y=2x+1,
把x=-1代入y=2x+1=-1,
故选A.
点评 本题主要考查对一次函数图象上点的坐标特征,理解题意并根据题意进行计算是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.从长度分别为2,4,6,7的四条线段中随机取三条,能构成三角形的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).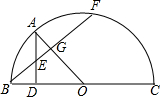 如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.
如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.