题目内容
把直线y=x+2向上平移n个单位后,与直线y=-2x+5的交点在第二象限,则n的取值范围是( )
| A、1<n<7 | B、n<5 |
| C、2<n<5 | D、n>3 |
考点:一次函数图象与几何变换
专题:
分析:直线y=x+2向上平移n个单位后可得:y=x+2+n,求出直线y=x+2+n与直线y=-2x+5的交点,再由此点在第二象限可得出n的取值范围.
解答:解:直线y=x+2向上平移n个单位后可得:y=x+2+n,
联立两直线解析式得:
,
解得:
,
即交点坐标为(
,
),
∵交点在第二象限,
∴
,
解得:n>3.
故选D.
联立两直线解析式得:
|
解得:
|
即交点坐标为(
| 3-n |
| 3 |
| 9+2n |
| 3 |
∵交点在第二象限,
∴
|
解得:n>3.
故选D.
点评:本题考查了一次函数图象与几何变换、两直线的交点坐标,注意第二象限的点的横坐标小于0、纵坐标大于0.

练习册系列答案
相关题目
 如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=3,则直线AB的函数表达式是( )
如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=3,则直线AB的函数表达式是( )| A、y=-2x+3 |
| B、y=-2x-3 |
| C、y=-2x+6 |
| D、y=-2x-6 |
北京与纽约的时差是+13小时,小亮于当地时间11月2日早8:00乘飞机从纽约到北京,纽约飞到北京需13小时,则到北京的时间为( )
| A、11月2日21:00 |
| B、11月2日10:00 |
| C、11月3日10:00 |
| D、11月3日8:00 |
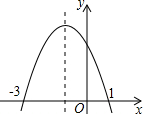 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象答下列问题: 已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|.
已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|. 有一圆柱,在圆柱下底的A点处有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行,如圆柱高为1dm,底面圆半径为2dm,则爬行的最短路程是
有一圆柱,在圆柱下底的A点处有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行,如圆柱高为1dm,底面圆半径为2dm,则爬行的最短路程是