题目内容
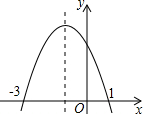 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象答下列问题:(1)方程ax2+bx+c=0的两个根是
(2)不等式ax2+bx+c>0的解集是
(3)y随x的增大而减小的自变量x的取值范围是
考点:二次函数与不等式(组),抛物线与x轴的交点
专题:
分析:(1)根据函数图象与x轴的交点写出即可;
(2)根据函数图象写出抛物线在x轴上方部分的x的取值范围即可;
(3)先求出函数图象的对称轴,然后写出对称轴右边部分的x的取值范围即可.
(2)根据函数图象写出抛物线在x轴上方部分的x的取值范围即可;
(3)先求出函数图象的对称轴,然后写出对称轴右边部分的x的取值范围即可.
解答:解:(1)由图可知,方程的两个根为x1=-3,x2=1;
(2)不等式ax2+bx+c>0的解集是-3<x<1;
(3)函数图象的对称轴为直线x=
=-1,
所以,y随x的增大而减小的自变量x的取值范围是x>-1.
故答案为:(1)x1=-3,x2=1;(2)-3<x<1;(3)x>-1.
(2)不等式ax2+bx+c>0的解集是-3<x<1;
(3)函数图象的对称轴为直线x=
| -3+1 |
| 2 |
所以,y随x的增大而减小的自变量x的取值范围是x>-1.
故答案为:(1)x1=-3,x2=1;(2)-3<x<1;(3)x>-1.
点评:本题考查了二次函数与不等式,抛物线与x轴的交点,此类题目,利用数形结合的思想求解更简便.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列方程是一元二次方程的是( )
| A、2x-y=1 | ||
| B、3x(x-1)=3x2+6 | ||
C、x+
| ||
| D、x2-3=0 |
把直线y=x+2向上平移n个单位后,与直线y=-2x+5的交点在第二象限,则n的取值范围是( )
| A、1<n<7 | B、n<5 |
| C、2<n<5 | D、n>3 |
 如图,在?ABCD中,E为DC边上一点,且BE=BC,求证:AE=BD.
如图,在?ABCD中,E为DC边上一点,且BE=BC,求证:AE=BD.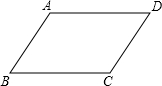 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可) 如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是
如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是