题目内容
 已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|.
已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|.(1)a3+b3的值.
(2)化简|a|-|a+b|-|c-a|+|c-b|-|-2b|.
考点:整式的加减,数轴,绝对值
专题:
分析:(1)由图可知,c<b<0<a,又|a|=|b|,则a与b互为相反数,根据相反数的性质得到a+b=0,a3+b3=0;
(2)根据绝对值的定义即可化简.
(2)根据绝对值的定义即可化简.
解答:解:(1)∵a>0,b<0,|a|=|b|,
∴a+b=0,a=-b,
∴a3+b3=0;
(2)∵c<b<0<a,a+b=0,
∴|a|-|a+b|-|c-a|+|c-b|-|-2b|
=a-0+c-a+b-c-(-2b)
=a+c-a+b-c+2b
=3b.
∴a+b=0,a=-b,
∴a3+b3=0;
(2)∵c<b<0<a,a+b=0,
∴|a|-|a+b|-|c-a|+|c-b|-|-2b|
=a-0+c-a+b-c-(-2b)
=a+c-a+b-c+2b
=3b.
点评:本题考查了整式的加减,数轴,绝对值及有理数的运算法则,是基础知识,比较简单.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
把直线y=x+2向上平移n个单位后,与直线y=-2x+5的交点在第二象限,则n的取值范围是( )
| A、1<n<7 | B、n<5 |
| C、2<n<5 | D、n>3 |
x的3倍减去2的差不大于0,列出不等式为( )
| A、3x-2≤0 |
| B、3x-2≥0 |
| C、3x-2<0 |
| D、3x-2>0 |
 如图,已知点A,B在双曲线y=
如图,已知点A,B在双曲线y=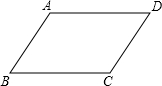 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可) 如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是
如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是