题目内容
关于x的一元二次方程(a-b)x2+(b-c)x+(c-a)=0的两根相等,则a,b,c关系为 .
考点:根的判别式,一元二次方程的定义
专题:
分析:由关于x的一元二次方程(a-b)x2+(b-c)x+(c-a)=0的两根相等,则a-b≠0,且△=0,即△=(b-c)2-4(a-b)(c-a)=(b+c)2-4a(b+c)+4a2=(b+c-2a)2=0,即可得到a,b,c的关系.
解答:解:∵方程(a-b)x2+(b-c)x+(c-a)=0为一元二次方程且有两根相等,
∴a-b≠0,且△=0,
即△=(b-c)2-4(a-b)(c-a)=(b+c)2-4a(b+c)+4a2=(b+c-2a)2=0,
故a≠b且b+c-2a=0,即b+c=2a,
所以a,b,c的关系为b+c=2a且a≠b.
故答案为:b+c=2a且a≠b.
∴a-b≠0,且△=0,
即△=(b-c)2-4(a-b)(c-a)=(b+c)2-4a(b+c)+4a2=(b+c-2a)2=0,
故a≠b且b+c-2a=0,即b+c=2a,
所以a,b,c的关系为b+c=2a且a≠b.
故答案为:b+c=2a且a≠b.
点评:此题主要考查了根的判别式以及一元二次方程的定义,熟练利用完全平方公式得出是解题关键.

练习册系列答案
相关题目
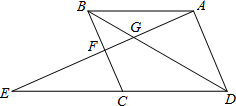 如图,点E为平行四边形ABCD中DC延长线上的一点,且CE=DC.连结AE,分别交BC、BD于点F、G.若BD=6,求DG的长.
如图,点E为平行四边形ABCD中DC延长线上的一点,且CE=DC.连结AE,分别交BC、BD于点F、G.若BD=6,求DG的长.