题目内容
7.阅读理解:配方中是中学数学的重要方法,用配方法可求最大(小)值.对于任意正实数a、b,可作如下变形:a+b=($\sqrt{a}$)2+($\sqrt{b}$)2=($\sqrt{a}$)2+($\sqrt{b}$)2-2 $\sqrt{ab}$+2$\sqrt{ab}$=($\sqrt{a}$-$\sqrt{b}$)2+2$\sqrt{ab}$,
又∵($\sqrt{a}$-$\sqrt{b}$)2≥0,∴($\sqrt{a}$-$\sqrt{b}$)2+2$\sqrt{ab}$≥0+2$\sqrt{ab}$,即a+b≥2$\sqrt{ab}$.
根据上述内容,回答下列问题:在a+b≥2$\sqrt{ab}$(a、b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a、b满足a=b时,a+b有最小值2$\sqrt{p}$.
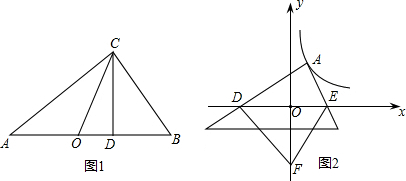
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a,DB=2b,试根据图形验证a+b≥2$\sqrt{ab}$成立,并指出等号成立时的条件.
(3)探索应用:如图2,已知A为反比例函数y=$\frac{4}{x}$的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
分析 (1)根据题中的例子即可直接得出结论;
(2)根据直角三角形的性质得出CO=a+b,CD=$\sqrt{ab}$,再由(1)中的结论即可得出等号成立时的条件;
(3)过点A作AH⊥x轴于点H,根据S四边形ADFE=S△ADE+S△FDE可知当DH=EH时DE最小,由此可得出结论.
解答 解:(1)∵a+b≥2$\sqrt{ab}$,a、b均为正实数,
∴当且仅当a、b满足a=b时,a+b有最小值.
故答案为:a=b;
(2)∵△ABC中,∠ACB=90°,CD⊥AB,CO为AB边上中线,AD=2a,DB=2b,
∴OC=$\frac{1}{2}$(AD+BD)=a+b,CD=2$\sqrt{ab}$,OC≥CD,即a+b≥2$\sqrt{ab}$,
∴当点D与点O重合时等式成立;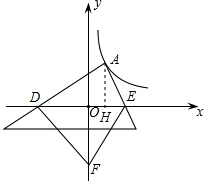
(3)如图所示,过点A作AH⊥x轴于点H,
∵S四边形ADFE=S△ADE+S△FDE=$\frac{1}{2}$DE•|yA|+$\frac{1}{2}$DE•OF=$\frac{1}{2}$DE(yA+OF),
∴当DH=EH时DE最小,
∴A点的横坐标为1,
∴AH=4,
∴DE最小为8,
∴S四边形ADFE=$\frac{1}{2}$×8×(4+3)=28.
点评 本题考查的是反比例函数综合题,涉及到用配方法可求最大(小)值,在a+b≥2$\sqrt{ab}$(a、b均为正实数)中,若ab为定值,则当且仅当a、b满足a=b时,a+b有最小值2$\sqrt{ab}$是解答此题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.
如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA. 如图,直线AB∥CD,与直线EF分别交于M,N,则图中与∠END相等的角(∠END除外)的个数为( )
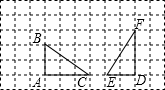
如图,直线AB∥CD,与直线EF分别交于M,N,则图中与∠END相等的角(∠END除外)的个数为( )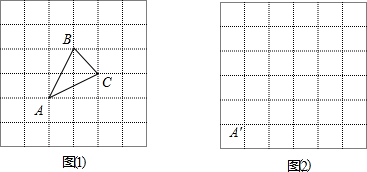
 如图方格纸中△ABC绕着点A逆时针旋转90度,再向右平移6格可得到△DEF.
如图方格纸中△ABC绕着点A逆时针旋转90度,再向右平移6格可得到△DEF.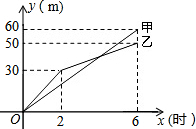 在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题: