题目内容
11．因式分解：（1）-16y4-32y3+8y2
（2）（x2+4）2-16x2．
（3）9（a-b）2+12（a2-b2）+4（a+b）2．
（4）（x2+4x）2+8（x2+4x）+16．
分析 （1）原式提取公因式即可得到结果；
（2）原式利用平方差公式及完全平方公式分解即可；
（3）原式利用完全平方公式分解即可；
（4）原式利用完全平方公式分解即可．
解答 解：（1）原式=-8y2（2y2+4y-1）；
（2）原式=（x2+4+4x）（x2+4-4x）=（x+2）2（x-2）2；
（3）原式=[3（a-b）]2+12（a+b）（a-b）+[2（a+b）]2=[3（a-b）+2（a+b）]2=（5a-b）2；
（4）原式=（x2+4x+4）2=（x+2）4．
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
1．
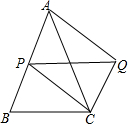如图，在△ABC中，∠BAC=45°，AB=AC=8，P为AB边上一动点，以PA、PC为边作平行四边形PAQC，则对角线PQ的最小值为（ ）
如图，在△ABC中，∠BAC=45°，AB=AC=8，P为AB边上一动点，以PA、PC为边作平行四边形PAQC，则对角线PQ的最小值为（ ）| A． | 6 | B． | 8 | C． | 2$\sqrt{2}$ | D． | 4$\sqrt{2}$ |
如图，直线AB∥CD，与直线EF分别交于M，N，则图中与∠END相等的角（∠END除外）的个数为（ ）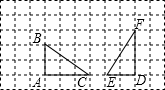
如图方格纸中△ABC绕着点A逆时针旋转90度，再向右平移6格可得到△DEF．
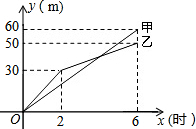在三河市创建文明城区的活动中，有两段长度相等的彩色道砖铺设任务，分别交给甲、乙两个施工队同时进行施工．如图是反映所铺设彩色道砖的长度y（米）与施工时间x（时）之间关系的部分图象．请解答下列问题：
