题目内容
13．已知菱形ABCD的边长是9，点E在直线AD上，DE=3，连接BE与对角线AC相交于点M，则$\frac{MC}{AM}$的值是（ ）| A． | 3：1 | B． | 4：3 | C． | 3：4 | D． | 3：4或3：2 |
分析 首先根据题意作图，注意分为E在线段AD上与E在AD的延长线上，然后由菱形的性质可得AD∥BC，则可证得△MAE∽△MCB，根据相似三角形的对应边成比例即可求得答案．
解答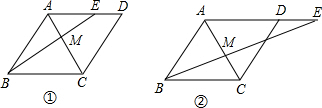 
解：∵菱形ABCD的边长是8，
∴AD=BC=9，AD∥BC，
如图1：当E在线段AD上时，
∴AE=AD-DE=9-3=6，
∴△MAE∽△MCB，
∴$\frac{MC}{AM}$=$\frac{9}{6}$=$\frac{3}{2}$；
如图2，当E在AD的延长线上时，
∴AE=AD+DE=9+3=12，
∴△MAE∽△MCB，
∴$\frac{MC}{AM}$=$\frac{9}{12}$=$\frac{3}{4}$．
∴$\frac{MC}{AM}$的值是$\frac{3}{2}$或$\frac{3}{4}$．
故选D．
点评 此题考查了菱形的性质，相似三角形的判定与性质等知识．解题的关键是注意此题分为E在线段AD上与E在AD的延长线上两种情况，小心不要漏解．
练习册系列答案
相关题目
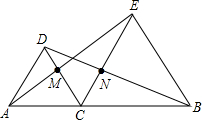如图，△DAC和△EBC均是等边三角形，A、C、B三点在一条直线上，AE、BD分别与CD、CE交于点M、N．
1．一个五次多项式与一个三次多项式的相加，所得结果的次数是（ ）
| A． | 八次 | B． | 五次 | C． | 三次 | D． | 不大于五次 |
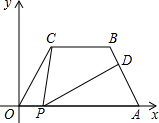如图，平面直角坐标系中，在四边形OABC中，BC∥OA，OC=AB，OA=7，AB=4，∠COA=60°，点P是x轴上一个动点，点P不与点O、A重合，连接CP，点D是边AB上一点，连接PD．