题目内容
5.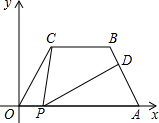 如图,平面直角坐标系中,在四边形OABC中,BC∥OA,OC=AB,OA=7,AB=4,∠COA=60°,点P是x轴上一个动点,点P不与点O、A重合,连接CP,点D是边AB上一点,连接PD.
如图,平面直角坐标系中,在四边形OABC中,BC∥OA,OC=AB,OA=7,AB=4,∠COA=60°,点P是x轴上一个动点,点P不与点O、A重合,连接CP,点D是边AB上一点,连接PD.(1)求点B的坐标;
(2)若△OCP是等腰三角形,求此时点P的坐标;
(3)当点P在边OA上,∠CPD=∠OAB,且$\frac{BD}{AB}$=$\frac{5}{8}$时,求此时点P的坐标.
分析 (1)过B作BF⊥OA,判断出∠BAO=60°,进而求出AF=$\frac{1}{2}$AB=2,BF=$\sqrt{3}$AF=2$\sqrt{3}$即可得出点B坐标,
(2)分三种情况利用等边三角形的性质即可求出点P的坐标;
(3)先判断出∠OCP=∠APB,进而得出△OPC∽△ADP,即$\frac{OP}{AD}=\frac{OC}{AP}$,另为求出AD,最后用得出的比例式建立方程求出OP即可得出结论.
解答 (1)如图1, 过B作BF⊥OA,
过B作BF⊥OA,
∵∠COA=60°,OC=AB,
∴∠BAO=60°,
∵AB=4,
∴AF=$\frac{1}{2}$AB=2,BF=$\sqrt{3}$AF=2$\sqrt{3}$,
∵AO=7,
∴OF=5,
∴$B({5\;,\;\;2\sqrt{3}})$,
(2)①当OC=OP=4时,
∴P(4,0),(-4,0)
②当OC=CP=4时,
∵∠COP=60°,
∴△OCP是等边三角形,
∴P(4,0),
③当CP=OP时,
∴∠OCP=∠COP=60°,
∴△COP是等边三角形,
∴∠P(4,0),
即:满足条件的点P的坐标为(4,0),(-4,0);
(3)∵∠CPD=∠OAB=60°,
∴∠COA=∠CPD=∠OAB,
∵∠AOC+∠OCP=∠APD+∠DPC,
∴∠OCP=∠APD,
∴△OPC∽△ADP,
∴$\frac{OP}{AD}=\frac{OC}{AP}$,
∴OP•AP=AD•OC,
∵$\frac{BD}{AB}=\frac{5}{8}$,
∴$BD=\frac{5}{2}$$AD=\frac{3}{2}$,
∴$OP•AP=\frac{3}{2}×4=6$,
∴OP•(7-OP)=6,
∴OP2-7OP+6=0,
∴OP1=1,OP2=6,
∴P(1,0)P(6,0).
点评 此题是相似形综合题,主要考查了等腰梯形的性质,含30°角的直角三角形的性质,等边三角形的性质,三角形外角的性质,解(1)的关键是求出AF和BF,解(2)的关键是分类讨论,解(3)的关键是判断出△OPC∽△ADP是一道中等难度的中考常考题.

| A. | 80(1+x)2=350 | B. | 80[1+(1+x)+(1+x)2]=350 | ||
| C. | 80+80×2(1+x)=350 | D. | 80+80×2x=350 |
| A. | 3:1 | B. | 4:3 | C. | 3:4 | D. | 3:4或3:2 |
 某绿化队承担一项绿化任务,工作一段时间后,提高了工作效率.该绿化队完成的绿化面积S(m2)与工作时间t(h)之间的函数关系如图所示,则该绿化队提高工作效率前每小时完成的绿化面积是( )
某绿化队承担一项绿化任务,工作一段时间后,提高了工作效率.该绿化队完成的绿化面积S(m2)与工作时间t(h)之间的函数关系如图所示,则该绿化队提高工作效率前每小时完成的绿化面积是( )| A. | 150m2 | B. | 300m2 | C. | 330m2 | D. | 450m2 |
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b<0 | D. | k<0,b>0 |
| A. | 2 | B. | -2 | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
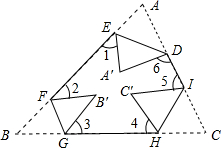 如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),图中∠1+∠2+∠3+∠4+∠5+∠6=360°.
如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),图中∠1+∠2+∠3+∠4+∠5+∠6=360°. 如图,在平面直角坐标系中,已知点A(0,3),且△OAB≌△O'A'B',点A的对应点A'在直线y=$\frac{3}{4}$x上,A'O'⊥x轴于O'点,则点B与其对应点B'间的距离为4.
如图,在平面直角坐标系中,已知点A(0,3),且△OAB≌△O'A'B',点A的对应点A'在直线y=$\frac{3}{4}$x上,A'O'⊥x轴于O'点,则点B与其对应点B'间的距离为4. 在一个可以改变体积的密闭容器内,装有一定质量的二氧化碳.当改变容器的体积时,气体的密度也会随之改变,密度ρ是体积V的反比例函数,它的图象如图所示.
在一个可以改变体积的密闭容器内,装有一定质量的二氧化碳.当改变容器的体积时,气体的密度也会随之改变,密度ρ是体积V的反比例函数,它的图象如图所示.