题目内容
4.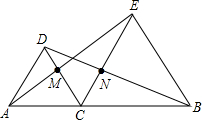 如图,△DAC和△EBC均是等边三角形,A、C、B三点在一条直线上,AE、BD分别与CD、CE交于点M、N.
如图,△DAC和△EBC均是等边三角形,A、C、B三点在一条直线上,AE、BD分别与CD、CE交于点M、N.现有如下结论:①AM=DN; ②EM=BN; ③∠CAM=∠CDN; ④∠CME=∠CNB.
(1)上述结论正确的有①②③④.
(2)选出一个你认为正确的结论,并证明这个结论.
你选的结论是:③.
证明:
∵△DAC和△EBC均是等边三角形,
∴AC=CD,∠ACD=∠BCE=60°,CE=CB,
∵A、C、B三点在一条直线上,
∴∠DCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB,
在△ACE和△DCB中,
∵$\left\{\begin{array}{l}{AC=CD}\\{∠ACE=∠DCB}\\{EC=BC}\end{array}\right.$
∴△ACE≌△DCB(SAS),
∴∠CAM=∠CDN,.
分析 (1)4个选项都正确;
(2)证明△ACE≌△DCB,得∠CAM=∠CDN,证明△ACM≌△DCN得:AM=DN,再证明△MCE≌△NCB(ASA),得EM=BN,∠CME=∠CNB.
解答 解:(1)上述结论正确的有:①②③④;
故答案为:①②③④;
(2)选③,
证明:∵△DAC和△EBC均是等边三角形,
∴AC=CD,∠ACD=∠BCE=60°,CE=CB,
∵A、C、B三点在一条直线上,
∴∠DCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB,
在△ACE和△DCB中,
∵$\left\{\begin{array}{l}{AC=CD}\\{∠ACE=∠DCB}\\{CE=CB}\end{array}\right.$,
∴△ACE≌△DCB(SAS),
∴∠CAM=∠CDN,
所以③正确;
选①,
证明:在△ACM和△DCN中,
∵$\left\{\begin{array}{l}{∠CAM=∠CDN}\\{AC=CD}\\{∠ACD=∠DCE=60°}\end{array}\right.$,
∴△ACM≌△DCN(ASA),
∴AM=DN,
所以①正确;
选②,
证明:∵△ACE≌△DCB,
∴∠MEC=∠NBC,
在△MCE和△NCB中,
∵$\left\{\begin{array}{l}{∠MCE=∠NCB}\\{EC=BC}\\{∠MEC=∠NBC}\end{array}\right.$,
∴△MCE≌△NCB(ASA),
∴EM=BN,∠CME=∠CNB.
所以②和④都正确.
点评 本题考查了三角形全等的性质和判定、等边三角形的性质,是常考题型,此类题变化多样,熟练掌握等边三角形的性质是关键,利用等边三角形的性质得出三角形全等的条件即可得出结论.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
14.点M在第二象限,它到x轴、y轴的距离分别为4和2,则点M的坐标为( )
| A. | (4,2) | B. | (-2,4) | C. | (-4,-2) | D. | (2,4) |
16.某科普网站从2009年10月1日起,连续登载新中国成立60周年来我国科技成果展,该网站的浏览量猛增.已知2009年10月份该网站的浏览量为80万人次,第四季度总浏览量为350万人次,如果浏览量平均每月增长率为x,则应列方程为( )
| A. | 80(1+x)2=350 | B. | 80[1+(1+x)+(1+x)2]=350 | ||
| C. | 80+80×2(1+x)=350 | D. | 80+80×2x=350 |
13.已知菱形ABCD的边长是9,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,则$\frac{MC}{AM}$的值是( )
| A. | 3:1 | B. | 4:3 | C. | 3:4 | D. | 3:4或3:2 |
14.如果x=0是关于x的方程3x-2a=4的解,则a的值是( )
| A. | 2 | B. | -2 | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
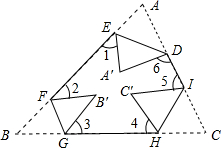 如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),图中∠1+∠2+∠3+∠4+∠5+∠6=360°.
如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),图中∠1+∠2+∠3+∠4+∠5+∠6=360°. 如图矩形ABCD中,AB=2,AD=4,矩形ABCD绕点A顺时针旋转90度,得到矩形AB′C′D′,则CC′=2$\sqrt{10}$.
如图矩形ABCD中,AB=2,AD=4,矩形ABCD绕点A顺时针旋转90度,得到矩形AB′C′D′,则CC′=2$\sqrt{10}$. 完成以下推理,并在括号中写出相应的根据
完成以下推理,并在括号中写出相应的根据