题目内容
16.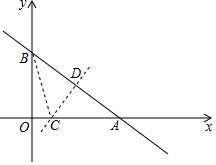 如图,直线y=-$\frac{3}{4}$x+6与x、y轴分别交于点A,B.
如图,直线y=-$\frac{3}{4}$x+6与x、y轴分别交于点A,B.(1)求点A和点B的坐标;
(2)将线段AB折叠,使点A与点B重合,折痕CD交x轴于点C,交AB于点D.求点C的坐标;
(3)在直线AB上是否存在点P,使△ACP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
分析 (1)分别令x=0,y=0,解方程即可解决问题.
(2)由CB=CA,设CB=AC=x,在Rt△OBC中,根据OB2+OC2=BC2,可得62+(8-x)2=x2,解方程即可.
(3)分三种情形①当CP1=CA时,P与B重合,②P2C=P2A时,∴y=-$\frac{3}{4}$×$\frac{39}{8}$+6=$\frac{75}{32}$,③当AP=AC时,分别求解即可.
解答 解:(1)对于y=-$\frac{3}{4}$x+6,
令x=0,得y=6,∴点B坐标(0,6),
令y=0得x=8,∴点A坐标(8,0).
(2)∵CB=CA,设CB=AC=x,
在Rt△OBC中,∵OB2+OC2=BC2,
∴62+(8-x)2=x2,
∴x=$\frac{25}{4}$,
∴OC=OA-AC=8-$\frac{25}{4}$=$\frac{7}{4}$,
∴点C坐标($\frac{7}{4}$,0).
(3)①当CP1=CA时,P与B重合,P1(0,6).
②P2C=P2A时,点P的横坐标为$\frac{39}{8}$,
∴y=-$\frac{3}{4}$×$\frac{39}{8}$+6=$\frac{75}{32}$,
∴P2($\frac{39}{8}$,$\frac{75}{32}$)
③当AP=AC时,P3(3,$\frac{15}{4}$)或P4(13,-$\frac{15}{4}$).
综上所述,点P坐标为(0,6)或($\frac{39}{8}$,$\frac{75}{32}$)或(3,$\frac{15}{4}$)或(13,-$\frac{15}{4}$).
点评 本题考查一次函数综合题、勾股定理、等腰三角形的判定和性质等知识,解题的关键是学会分类讨论,注意不能漏解,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案 已知二次函数y=-x2+2x+3.
已知二次函数y=-x2+2x+3.