题目内容
11. 已知二次函数y=-x2+2x+3.
已知二次函数y=-x2+2x+3.(1)求抛物线顶点M的坐标;
(2)设抛物线与x轴交于A,B两点,与y轴交于C点,求A,B,C的坐标(点A在点B的左侧),并画出函数图象的大致示意图;
(3)根据图象,写出不等式-x2+2x+3>0的解集.
分析 (1)将二次函数解析式整理成顶点式形式,然后写出点M的坐标即可;
(2)令y=0求出点A、B的坐标,令x=0求出点C的坐标,然后作出二次函数大致图象即可;
(3)根据函数图象写出抛物线在x轴上方部分的x的取值范围即可.
解答 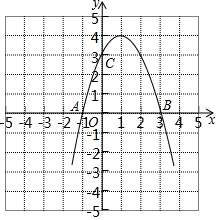 解:(1)∵y=-x2+2x+3=-(x-1)2+4,
解:(1)∵y=-x2+2x+3=-(x-1)2+4,
∴顶点M的坐标为(1,4);
(2)令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3,
∵点A在点B的左侧,
∴A(-1,0),B(3,0),
令x=0,则y=3,
∴点C的坐标为(0,3),
函数图象的大致示意图如图;
(3)由图可知,不等式-x2+2x+3>0的解集为-1<x<3.
点评 本题考查了二次函数与不等式,抛物线与x轴的交点问题,数形结合是数学中的重要思想之一,解决函数问题更是如此.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.扬州市第26路公交车沿文昌路东西方向行驶,如果把石塔寺站台记为0,向东行驶记为正,向西行驶记为负,其中一辆车从石塔寺站台出发以后行驶的路程如表(单位:km):
(1)该车最后是否回到了石塔寺?为什么?
(2)该辆车离开出发点最远是多少千米?
(3)这辆车在上述过程中一共行驶了多少路程?
(4)若汽车耗油量为3升/千米,共耗油多少升?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
(2)该辆车离开出发点最远是多少千米?
(3)这辆车在上述过程中一共行驶了多少路程?
(4)若汽车耗油量为3升/千米,共耗油多少升?
6. 如图,△ABC三个顶点的坐标分别为A(-2,5),B(-5,1),C(-2,1),将△ABC绕点C按顺时针方向旋转90°,得到△DEC,则点D的坐标为( )
如图,△ABC三个顶点的坐标分别为A(-2,5),B(-5,1),C(-2,1),将△ABC绕点C按顺时针方向旋转90°,得到△DEC,则点D的坐标为( )
 如图,△ABC三个顶点的坐标分别为A(-2,5),B(-5,1),C(-2,1),将△ABC绕点C按顺时针方向旋转90°,得到△DEC,则点D的坐标为( )
如图,△ABC三个顶点的坐标分别为A(-2,5),B(-5,1),C(-2,1),将△ABC绕点C按顺时针方向旋转90°,得到△DEC,则点D的坐标为( )| A. | (1,2) | B. | (2,1) | C. | (1,1) | D. | (2,2) |
 如图是几个正方体所组成的几何体从上面看到的图形,小正方形中的数字表示该位置小正方块的个数.请画出这个几何体的从正面和左面看到的图形.
如图是几个正方体所组成的几何体从上面看到的图形,小正方形中的数字表示该位置小正方块的个数.请画出这个几何体的从正面和左面看到的图形.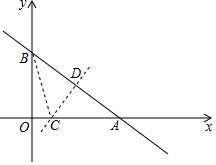 如图,直线y=-$\frac{3}{4}$x+6与x、y轴分别交于点A,B.
如图,直线y=-$\frac{3}{4}$x+6与x、y轴分别交于点A,B.
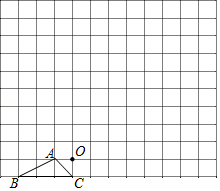 图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.