题目内容
内角和等于外角和2倍的多边形是（ ）
A. 五边形 B. 六边形 C. 七边形 D. 八边形
B
【解析】试题分析：本题应先设这个多边形的边数为n，则依题意可列出方程（n﹣2）×180°=360°×2，从而解出n=6，即这个多边形的边数为6．
【解析】
设这个多边形的边数为n，则依题意可得：
（n﹣2）×180°=360°×2，
解得n=6，
∴这个多边形的边数为6．
故选B．
用配方法把二次函数y＝l+2x－x2化为y＝a(x－h)2+k的形式，作出它的草图，回答下列问题．
(1)求抛物线的顶点坐标和它与x轴的交点坐标；
(2)当x取何值时，y随x的增大而增大?
(3)当x取何值时，y的值大于0?
y=－(x－1)2＋2(1)顶点坐标为(1，2)，与x轴的两个交点坐标分别为(1－，0)，(1＋，0)(2)当x＜1时，y随x的增大而增大.(3)当l－＜x＜1＋时，y的值大于0
【解析】分析：（1）利用配方法得到y=-(x-1)²+2，则根据二次函数的性质可得到抛物线的顶点坐标；再利用抛物线与x轴的交点问题，通过解方程-(x-1)²+2=0可得到它与x轴的交点坐标；（2）根据二次函数的性质... 如图，在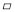
ABCD中，点E在CD边上运动(不与C，D两点重合)，连结AE并延长与BC的延长线交于点F.连结BE，DF，若△BCE的面积为8，则△DEF的面积为________．
8
【解析】试题解析：
故答案为： 如图，P为平行四边形ABCD的边AD上的一点，E，F分别为PB，PC的中点，△PEF，△PDC，△PAB的面积分别为S，S1，S2．若S=3，则S1+S2的值为（ ）
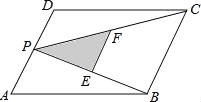
A．24 B．12 C．6 D．3
B
【解析】
试题分析：过P作PQ∥DC交BC于点Q，由DC∥AB，得到PQ∥AB，
∴四边形PQCD与四边形APQB都为平行四边形，
∴△PDC≌△CQP，△ABP≌△QPB，
∴S△PDC=S△CQP，S△ABP=S△QPB，
∵EF为△PCB的中位线，
∴EF∥BC，EF=BC，
∴△PEF∽△PBC，且相似比为1：2，
∴S△PEF：S... 如果一个多边形的内角和与它的外角和相等，那么这个多边形是____边形
四
【解析】∵多边形的外角和为360°，
而一个多边形的内角和与它的外角和正好相等，设这个多边形为n边形，
∴（n-2）•180°=360°，
∴n=4，
故答案为：四． 若一个多边形除了一个内角外,其余各内角之和是2570°,则这个角是( )
A. 90° B. 15° C. 120° D. 130°
D
【解析】设这个内角度数为x°，边数为n，
则（n-2）×180-x=2570，
180•n=2930+x，
∵n为正整数，
∴n=17，
∴去掉角度数为180°×（17-2）-2570°=130°，
故选D. 某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).
(1)扶梯在外面的部分有多少级.
(2)如果扶梯附近有一从二楼下到一楼的楼梯,台阶级数与扶梯级数相等,这两人各自到扶梯顶部后按原速度走下楼梯,到一楼后再乘坐扶梯(不考虑扶梯与楼梯间的距离).则男孩第一次追上女孩时,他走了多少台阶?
(1)楼梯有54级(2) 198级
【解析】【试题分析】
(1)设女孩速度为级/分,电梯速度为级/分,楼梯(扶梯)为级,则男孩速度为级/分, 根据时间相等列方程，有：
①两式相除,得,解方程得即可.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯次,走过楼梯次,则这时女孩走过扶梯次,走过楼梯次.
将代入方程组①,得,即男孩乘扶梯上楼的速度为级/分,... 公路全长为skm，骑自行车t小时可到达，为了提前半小时到达，骑自行车每小时应多走_____________.
－
【解析】公路全长为skm，骑自行车t小时可到达，则速度为 若提前半小时到达，则速度为 则现在每小时应多走（ ） 小明解方程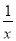
－
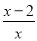=1的过程如下：
【解析】
方程两边乘x，得1－（x－2）=1.①
去括号，得1－x－2=1.②
移项，得－x=1－1+2.③
合并同类项，得－x=2.④
解得x=－2.⑤
所以，原分式方程的解为x=－2.⑥
请指出他解答过程中的错误，并写出正确的解答过程．
见解析
【解析】试题分析：去分母时，注意是否每一项都乘以x，去括号，移项时，注意符合的变化；最后注意分式方程一定要检验方程的解。
【解析】
小明的解法有三处错误，步骤①去分母有误； 步骤②去括号有误；步骤⑥少检验.
正确解法为：方程两边乘x，得1－（x－2）=x.
去括号，得1－x+2=x.
移项，得－x－x=－1－2.
合并同类项，得－2x=－3.
解...