题目内容
1.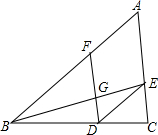 如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )
如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )| A. | $\frac{AF}{AB}$=$\frac{EG}{BE}$ | B. | $\frac{FG}{GD}$=$\frac{BG}{GE}$ | C. | $\frac{FG}{AE}$=$\frac{DG}{EC}$ | D. | $\frac{AF}{BF}$=$\frac{AE}{EC}$ |
分析 根据四边形AFDE是平行四边形,于是得到DF∥AC,DE∥AF,即可得到结论$\frac{AF}{AB}=\frac{GE}{BE}$,$\frac{FG}{GD}=\frac{BG}{GE}$,故A,B正确,由DF∥AC,得到$\frac{FG}{AE}=\frac{BG}{BE}$,$\frac{DG}{CE}=\frac{BG}{BE}$,等量代换得到$\frac{FG}{AE}=\frac{DG}{EC}$,故C正确;由DF∥AC,推出$\frac{AF}{BF}=\frac{CD}{BD}$≠$\frac{AE}{CE}$,故D错误;
解答 解:∵四边形AFDE是平行四边形,
∴DF∥AC,DE∥AF,
∴$\frac{AF}{AB}=\frac{GE}{BE}$,$\frac{FG}{GD}=\frac{BG}{GE}$,故A,B正确,
∵DF∥AC,
∴$\frac{FG}{AE}=\frac{BG}{BE}$,$\frac{DG}{CE}=\frac{BG}{BE}$,
∴$\frac{FG}{AE}=\frac{DG}{EC}$,故C正确;
∵DF∥AC,
∴$\frac{AF}{BF}=\frac{CD}{BD}$≠$\frac{AE}{CE}$,故D错误;
故选D.
点评 本题考查了平分线分线段成比例,熟练掌握平行线分线段成比例定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列变形不正确的是( )
| A. | 由-$\frac{x}{2}$=0得x=0 | B. | 由2x+3=0得x=-$\frac{3}{2}$ | C. | 由3x=-2得x=-$\frac{2}{3}$ | D. | 由$\frac{3}{4}$x=2得x=$\frac{3}{2}$ |
11.下列计算正确的是( )
| A. | $\sqrt{20}=2\sqrt{10}$ | B. | $\sqrt{9}=±3$ | C. | $\sqrt{4}-\sqrt{2}=\sqrt{2}$ | D. | $\sqrt{(-5)^{2}}$=5 |
 如图,⊙A、⊙B、⊙C、⊙D两两外离,它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的面积之和是π.
如图,⊙A、⊙B、⊙C、⊙D两两外离,它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的面积之和是π.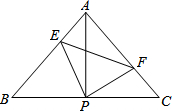 已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出的以下四个结论:
已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出的以下四个结论:
 如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1,画出三角形A1B1C1,并分别写出点A1、B1、C1的坐标.
如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1,画出三角形A1B1C1,并分别写出点A1、B1、C1的坐标.