题目内容
11.关于x的一元二次方程ax2+bx+c=0(a≠0),给出以下说法:(1)若△=b2-4ac>0,则方程cx2+bx+a=0一定有两个不相等的实根
(2)若x0是方程的一个根,△=(2ax0+b)2
(3)若b2>5ac,在方程一定有两个不相等的实数根
(4)若b=2a+3c,则方程必有两个不相等的实数根
其中,正确说法的序号是(2)(3)(4).
分析 (1)方程ax2+bx+c=0有两个不等的实数根,则△=b2-4ac>0,当c=0时,cx2+bx+a=0不成立;
(2)用求根公式表示x0.
(3)根据b2>5ac可以得到b2-4ac>0,从而证得方程ax2+bx+c=0一定有两个不相等的实数根.
(4)把b=2a+3c代入b2-4ac计算得到(2a+3b)2-4ac=4a2+8ac+9b2=4(a+c)2+5c2,而a≠0,则有b2-4ac>0,于是可对(4)进行判断.
解答 解:(1)当c=0时不成立;
(2)若x0是一元二次方程ax2+bx+c=0的根,可得x0=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$,把x0的值代入(2ax0+b)2,可得b2-4ac=(2ax0+b)2;
(3)∵b2>5ac,∴b2-5ac>0,∴b2-4ac>0,∴方程ax2+bx+c=0一定有两个不相等的实数根.
(4)当2a+3c=b,则b2-4ac=(2a+3b)2-4ac=4a2+8ac+9b2=4(a+c)2+5c2,而a≠0,于是b2-4ac>0,则方程必有两个不相等的实数根.
正确的是(2)、(3)、(4).
故答案为:(2)(3)(4).
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
3. 如图,数轴上表示数-2的相反数的点是( )
如图,数轴上表示数-2的相反数的点是( )
 如图,数轴上表示数-2的相反数的点是( )
如图,数轴上表示数-2的相反数的点是( )| A. | 点N | B. | 点M | C. | 点Q | D. | 点P |
1.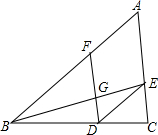 如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )
如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )
 如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )
如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )| A. | $\frac{AF}{AB}$=$\frac{EG}{BE}$ | B. | $\frac{FG}{GD}$=$\frac{BG}{GE}$ | C. | $\frac{FG}{AE}$=$\frac{DG}{EC}$ | D. | $\frac{AF}{BF}$=$\frac{AE}{EC}$ |
 如图,某校准备周末组织师生参观湖光岩,现有甲乙两家旅行社的收费y甲,y乙与x(x为参观人数)的函数关系如图所示,根据图象信息,回答下列问题:
如图,某校准备周末组织师生参观湖光岩,现有甲乙两家旅行社的收费y甲,y乙与x(x为参观人数)的函数关系如图所示,根据图象信息,回答下列问题: