题目内容
6.阅读下面材料:点A、B在数轴上分别表示数a,b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图(1),当A、B两点都不在原点时,①如图(2),点A、B都在原点的右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;②如图(3),点A、B都在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(a)=|a-b|;③如图(4),点A、B都在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(-b)=|a-b|;综上,数轴上A、B两点之间的距离|AB|=|a-b|.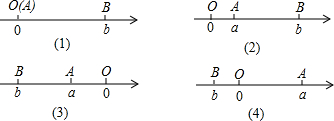
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是3;
(2)数轴上表示-1和-5的两点之间的距离是4;
(3)数轴上表示1和-4的两点之间的距离是5;
(4)数轴上表示x和-1的两点A之和B之间的距离是|x+1|,如果|AB|=2,那么x的值是-3或1.
分析 根据题意可知两点之间的距离等于这两个点表示数的差的绝对值.
解答 解:(1)数轴上表示2和5的两点之间的距离=|5-2|=3;
(2)数轴上表示-1和-5的两点之间的距离=|-5-(-1)|=|-5+1|=4;
(3)数轴上表示1和-4的两点之间的距离=|-4-1|=|-5|=5;
(4)数轴上表示x和-1的两点A之和B之间的距离=|x+1|,
因为在数轴上到表示-1的点的距离为2的数有两个它们是-3和1,所以x的值为-3或1.
故答案为:(1)3;(2)4;(3)5;(4)|x+1|;-3或1.
点评 本题主要考查的是绝对值的应用和数轴的认识,读懂题意,掌握两点之间距离的计算公式是解题的关键.

练习册系列答案
相关题目
1.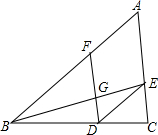 如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )
如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )
 如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )
如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,连接BE、DF交于点G,连接DE.若四边形AFDE是平行四边形,则下列说法错误的是( )| A. | $\frac{AF}{AB}$=$\frac{EG}{BE}$ | B. | $\frac{FG}{GD}$=$\frac{BG}{GE}$ | C. | $\frac{FG}{AE}$=$\frac{DG}{EC}$ | D. | $\frac{AF}{BF}$=$\frac{AE}{EC}$ |
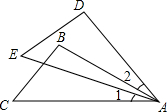 如图,△ABC≌△ADE,∠1=30°,则∠2=30°.
如图,△ABC≌△ADE,∠1=30°,则∠2=30°.