题目内容
1.已知正比例函数y=(k-1)x|k|,则k=-1.分析 根据正比例函数的定义,令|k|=1且k-1≠0即可.
解答 解:∵函数y=(k-1)x|k|是正比例函数,
则|k|=1且k-1≠0
解得k=±1且k≠1;
∴k=-1.
故答案为-1.
点评 本题主要考查了正比例函数的定义,及一般形式,是一个常见的题目类型.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
11.二次函数y=x2-4x+1的顶点坐标为( )
| A. | (2,5) | B. | (-2,5) | C. | (2,-3) | D. | (-2,-3) |
12.已知$\frac{a}{b}=\frac{2}{3}$,那么$\frac{a+b}{b}$=( )
| A. | $\frac{5}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{3}{5}$ |
16.下列各式中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | ±$\sqrt{25}$=5 | C. | $\sqrt{{{(-3)}^2}}$=-3 | D. | $\root{3}{-27}$=-3 |
13.在△ABC中,如果tanA=1,cosB=$\frac{{\sqrt{2}}}{2}$,则以下对△ABC形状的判断最确切的是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
11.学校开展为贫困地区捐书活动,以下是六名学生捐书的册数:2,2,2,3,3,6,则这组数据的方差为( )
| A. | 2 | B. | 2.5 | C. | 3 | D. | 3.5 |
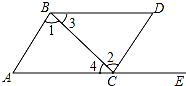 如图,从给出的四个条件:
如图,从给出的四个条件: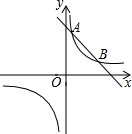 如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=-x+3的图象交于A(1,m),B(n,1)两点.
如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=-x+3的图象交于A(1,m),B(n,1)两点.