题目内容
10.解方程:(1)x2+3x=4
(2)x2-3x+1=0.
分析 (1)利用因式分解法将原方程变为(x-1)(x+4)=0,然后解得方程即可;
(2)观察方程可知运用公式法解得此方程比较简便,因为a=1,b=-3,c=1,再根据x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2b}$即可解得方程的解.
解答 解:(1)∵x2+3x-4=0,
∴(x-1)(x+4)=0,
∴x-1=0或x+4=0,
∴x1=1,x2=-4,
(2)∵x2-3x+1=0,
∴a=1,b=-3,c=1,
∴b2-4ac=(-3)2-4×1×1=5>0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{3±\sqrt{5}}{2×1}$=$\frac{3±\sqrt{5}}{2}$,
∴x1=$\frac{3+\sqrt{5}}{2}$,x2=$\frac{3-\sqrt{5}}{2}$.
点评 本题主要考察了一元二次方程的解法:因式分解法,公式法,配方法,仔细观察方程找到合理的方法解得方程是关键.

练习册系列答案
相关题目
5.某购物中心一月份的营业额为100万元,三月份的营业额为121万元,设每月的平均增长率为x,则可列方程为( )
| A. | 121(1-x)2=100 | B. | 121(1+x)2=100 | C. | 100(1-x)2=121 | D. | 100(1+x)2=121 |
15. 一只茶壶如图所示放置,从正面看到的几何体的形状图是( )
一只茶壶如图所示放置,从正面看到的几何体的形状图是( )
 一只茶壶如图所示放置,从正面看到的几何体的形状图是( )
一只茶壶如图所示放置,从正面看到的几何体的形状图是( )| A. |  | B. |  | C. |  | D. |  |
19.一次同学聚会,小李、小王、小明、小红4人见面,若他们每两人之间总要握手一次,则一共握手的次数是( )
| A. | 4次 | B. | 6次 | C. | 8次 | D. | 10次 |
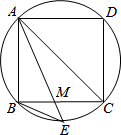 如图,在边长为4cm的圆内接正方形ABCD中,AC是对角线,M为边BC的中点,延长AM交圆于点E.
如图,在边长为4cm的圆内接正方形ABCD中,AC是对角线,M为边BC的中点,延长AM交圆于点E. 如图,点A、O、B在一条直线上,且∠BOC=119°40′,OD平分∠AOC,则∠AOD的度数为30°10′.
如图,点A、O、B在一条直线上,且∠BOC=119°40′,OD平分∠AOC,则∠AOD的度数为30°10′.