题目内容
15.(1)如图①,△ABC是锐角三角形,高BD、CE相交于点H,找出∠BHC和∠A之间存在何种等量关系;(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD、CE所在的直线相交于点H,把图②补充完整,并指出此时(1)中的等量关系是否仍然成立?
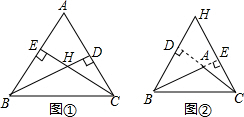
分析 (1)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案;
(2)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案.
解答 解:(1)由∠BHC与∠EHD是对顶角,得
∠BHC=∠EHD.
由高BD、CE相交于点H,得
∠ADH=∠AEH=90°.
由四边形内角和定理,得
∠A+∠AEH+∠EHD+∠HDA=360°,
∠A+∠EHD=360°-∠AEH-∠HDA=360°-90°-90°=180°,
∴∠BHC+∠A=180°;
(2)由∠BHC与∠EHD是对顶角,得
∠BHC=∠EHD.
由高BD、CE相交于点H,得
∠ADH=∠AEH=90°.
由四边形内角和定理,得
∠H+∠AEH+∠EHD+∠HDA=360°,
∠H+∠DAE=360°-∠AEH-∠HDA=360°-90°-90°=180°,
∴∠BHC+∠BAC=180°.
点评 本题考查了多边形的内角与外角,利用了四边形的内角和,对顶角的性质.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
4.下列各组数中,相等的一组是( )
| A. | (-3)3与-33 | B. | (-3)2与-32 | C. | (-3×2)3与3×(-2)3 | D. | -32与(-3)+(-3) |
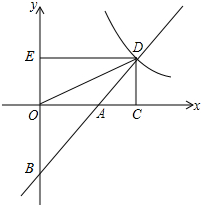 如图,直线y=x+b(b<0)与两坐标轴分别交于A,B两点,与双曲线y=$\frac{2}{x}(x>0)$交于点D,过点D作两坐标轴的垂线DC,DE,连结OD.
如图,直线y=x+b(b<0)与两坐标轴分别交于A,B两点,与双曲线y=$\frac{2}{x}(x>0)$交于点D,过点D作两坐标轴的垂线DC,DE,连结OD.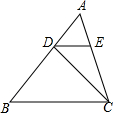 如图,已知:点D、E分别在△ABC的边AB、AC上,DE∥BC,AD:BD:AC=1:2:$\sqrt{3}$,BC=12厘米.
如图,已知:点D、E分别在△ABC的边AB、AC上,DE∥BC,AD:BD:AC=1:2:$\sqrt{3}$,BC=12厘米.
 如图,以AB为直径的圆中,点C为直径AB上任意一点,若分别以AC,BC为直径画半圆,且AB=6cm,求所得两半圆的长度之和.
如图,以AB为直径的圆中,点C为直径AB上任意一点,若分别以AC,BC为直径画半圆,且AB=6cm,求所得两半圆的长度之和.