题目内容
20.用“>”“<”或“=”号填空:(1)如果a<0,b>0,那么a•b<0,$\frac{a}{b}$<0;
(2)如果a>0,b<0,那么a•b<0,$\frac{a}{b}$<0;
(3)如果a<0,b<0,那么a•b>0,$\frac{a}{b}$>0;
(4)如果a=0,b≠0,那么a•b=0,那么$\frac{a}{b}$=0.
分析 原式各项利用有理数的乘除法则判断即可.
解答 解:(1)如果a<0,b>0,那么a•b<0,$\frac{a}{b}$<0;
(2)如果a>0,b<0,那么a•b<0,$\frac{a}{b}$<0;
(3)如果a<0,b<0,那么a•b>0,$\frac{a}{b}$>0;
(4)如果a=0,b≠0,那么a•b=0,那么$\frac{a}{b}$=0.
故答案为:(1)<;<;(2)<;<;(3)>;>;(4)=;=.
点评 此题考查了有理数的乘除法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
10.如图1所示,E、F分别为透明正方体的面ADD1A1,面BCC1B1的中心,则四边形BFD1E的正视图、左视图、俯视图分别是图2中的( )
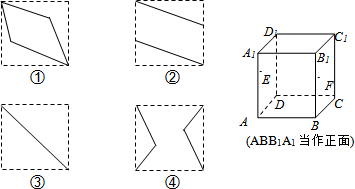

| A. | ②③② | B. | ①②① | C. | ①②③ | D. | ②③④ |
8.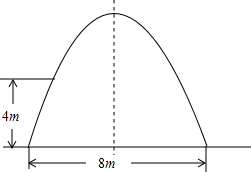 如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )
如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )
 如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )
如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )| A. | 6.0m | B. | 5.3m | C. | 5.6m | D. | 5.9m |
5. 已知二次函数y=ax2+bx+c的图象如图所示,则关于x的方程ax2+bx+c-3=0的根的情况是( )
已知二次函数y=ax2+bx+c的图象如图所示,则关于x的方程ax2+bx+c-3=0的根的情况是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则关于x的方程ax2+bx+c-3=0的根的情况是( )
已知二次函数y=ax2+bx+c的图象如图所示,则关于x的方程ax2+bx+c-3=0的根的情况是( )| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有两个不相等的负根 | D. | 有两个不相等的正根 |
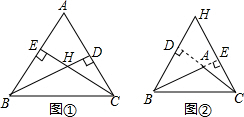

 如图,填空:
如图,填空: