题目内容
 我县为了倡导居民节约用水,生活用自来水按阶梯式水价计费,如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象,请根据图象所提供的信息,解答下列问题
我县为了倡导居民节约用水,生活用自来水按阶梯式水价计费,如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象,请根据图象所提供的信息,解答下列问题(1)用水量不超过10吨时每吨水收费多少元?
(2)当用水量超过10吨且不超过25吨时,求y与x之间的函数关系式;
(3)已知某户居民上月水费为55元,求这户居民上月用水多少吨?
考点:一次函数的应用
专题:
分析:(1)根据图示直接写出答案;
(2)根据图示知,该直线经过点(10,20),(25,70),则由待定系数法来求y与x之间的函数关系式;
(3)把y=55代入(2)中的函数关系式,求得x的值即可.
(2)根据图示知,该直线经过点(10,20),(25,70),则由待定系数法来求y与x之间的函数关系式;
(3)把y=55代入(2)中的函数关系式,求得x的值即可.
解答:解:(1)如图所示,用水量不超过10吨时每吨水收费为:20÷10=2(元/吨).
答:用水量不超过10吨时,水费为2元/吨;
(2)设y=kx+b(k≠0).
由图象知,该直线经过点(10,20),(25,70),则依题意得
,
解得
.
所以y与x之间的函数关系式是:y=
x-
(10<x≤25);
(3)当y=55时,
x-
=55,
解得x=20.5.
所以该户居民上月用水是20.5吨.
答:用水量不超过10吨时,水费为2元/吨;
(2)设y=kx+b(k≠0).
由图象知,该直线经过点(10,20),(25,70),则依题意得
|
解得
|
所以y与x之间的函数关系式是:y=
| 10 |
| 3 |
| 40 |
| 3 |
(3)当y=55时,
| 10 |
| 3 |
| 40 |
| 3 |
解得x=20.5.
所以该户居民上月用水是20.5吨.
点评:本题考查了一次函数的应用.此题要求学生具备一定的读图能力.

练习册系列答案
相关题目
若点P(x,y)的坐标满足方程组
,则点P不可能在( )
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
一个矩形的长和宽分别是3
、2
,则它的面积是( )
| 6 |
| 3 |
A、20
| ||
B、18
| ||
C、17
| ||
D、16
|
下列根式中,最简二次根式是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
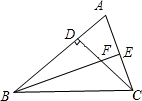 在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,并于CD相交于点F.
在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,并于CD相交于点F.