题目内容
8.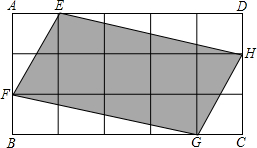 如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积为$\frac{5}{3}$.
如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积为$\frac{5}{3}$.
分析 设每个小正方形的边形为a,根据三角形的面积公式即可求出S△AEF、S△CGH、S△BFG、S△DHE的值,由此即可用含a2的代数式表示出四边形EFGH的面积,再根据四边形EFGH的面积为1即可求出a2,将其×15即可得出结论.
解答 解:设每个小正方形的边形为a,则:S△AEF=S△CGH=$\frac{1}{2}$a•2a=a2,S△BFG=S△DHE=$\frac{1}{2}$a•4a=2a2,
∴四边形EFGH的面积=15a2-S△AEF-S△CGH-S△BFG-S△DHE=9a2=1,
∴a2=$\frac{1}{9}$,
∴矩形ABCD的面积=15a2=15×$\frac{1}{9}$=$\frac{5}{3}$.
故答案为:$\frac{5}{3}$.
点评 本题考查了矩形的性质、三角形的面积、矩形的面积以及解一元二次方程,根据四边形EFGH的面积为1求出a2是解题的关键.

练习册系列答案
相关题目
18.x取任意实数,多项式2x-x2-2的值必定是( )
| A. | 正实数 | B. | 负实数 | C. | 非正实数 | D. | 非负实数 |
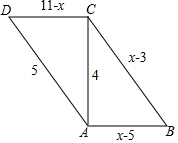 如图,在四边形ABCD中,AB=x-5,CD=11-x,AD=5,BC=x-3,对角线AC=4,AC⊥AB,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=x-5,CD=11-x,AD=5,BC=x-3,对角线AC=4,AC⊥AB,求证:四边形ABCD是平行四边形.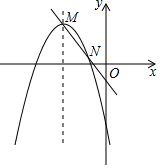 如图,已知抛物线y=-x2+px+q的对称轴为x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为(0,2).
如图,已知抛物线y=-x2+px+q的对称轴为x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为(0,2).