题目内容
3.已知三个非负实数a,b,c,满足3a+2b+c=5,2a+b-3c=1,若s=3a+b-7c的最大值为m,最小值为n,则mn=-$\frac{5}{77}$.分析 联立两等式后求出a与b,然后将a与b代入s中,化为一次函数最值问题,利用非负实数求出c的范围即可求出m与n的值.
解答 解:联立$\left\{\begin{array}{l}{3a+2b=5-c}\\{2a+b=1+3c}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=7c-3}\\{b=7-11c}\end{array}\right.$
∵a、b、c都是非负实数,
∴$\left\{\begin{array}{l}{7c-3≥0}\\{7-11c≥0}\\{c≥0}\end{array}\right.$
解得:$\frac{3}{7}$≤c≤$\frac{7}{11}$
∴s=3a+b-7c
=3(7c-3)+(7-11c)-7c
=3c-2
∴当c=$\frac{7}{11}$时,
s的最大值为:m=-$\frac{1}{11}$,
当c=$\frac{3}{7}$时,
s的最小值为:n=-$\frac{5}{7}$
∴mn=$\frac{5}{77}$
故答案为:$\frac{5}{77}$
点评 本题考查一次函数的综合问题,解题的关键是列出方程组求出a与b的表达式,然后利用一元一次不等式组求出c的范围,本题属于中等题型.

练习册系列答案
相关题目
12.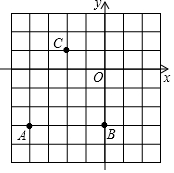 已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),C点关于y轴对称的点为C′,若设△ABC的面积为S1,△ACC′的面积为S2,则S1,S2的大小关系为( )
已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),C点关于y轴对称的点为C′,若设△ABC的面积为S1,△ACC′的面积为S2,则S1,S2的大小关系为( )
 已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),C点关于y轴对称的点为C′,若设△ABC的面积为S1,△ACC′的面积为S2,则S1,S2的大小关系为( )
已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),C点关于y轴对称的点为C′,若设△ABC的面积为S1,△ACC′的面积为S2,则S1,S2的大小关系为( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | 不能确定 |
13.下面是一名同学所做5道练习题:①(-3)0=1,②a3+a3=a6,③(-a5)÷(-a3)=-a2,④4m-2=$\frac{1}{4{m}^{2}}$,⑤(xy2)3=x3y6,他对的题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
12.下列代数式中,不是整式的是( )
| A. | $\frac{{a}^{2}b}{3}$ | B. | $\frac{a+1}{4}$ | C. | 0 | D. | $\frac{{a}^{2}+b}{a}$ |
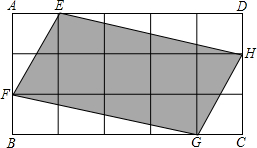 如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积为$\frac{5}{3}$.
如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积为$\frac{5}{3}$.