题目内容
17．
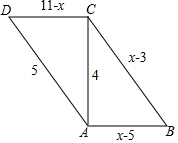如图，在四边形ABCD中，AB=x-5，CD=11-x，AD=5，BC=x-3，对角线AC=4，AC⊥AB，求证：四边形ABCD是平行四边形．
分析 首先利用勾股定理可得（x-5）2+42=（x-3）2，再解可得x的值，然后可算出CD、AB、BC的长，再根据两组对边分别相等的四边形是平行四边形可得结论．
解答 证明：∵AC⊥AD，
∴∠DAC=90°，
∴AD2+AC2=DC2，
∴（x-5）2+42=（x-3）2，
解得：x=8，
∴AB=3，CD=3，BC=5，
∵AD=5，
∴DC=AB，AD=BC，
∴四边形ABCD是平行四边形．
点评 此题主要考查了平行四边形的判定，以及勾股定理的应用，关键是掌握两组对边分别相等的四边形是平行四边形．
练习册系列答案
相关题目
7．下列说法正确的是（ ）
| A． | 0不是单项式 | B． | x没有系数 | C． | x2+$\frac{1}{x}$是多项式 | D． | -$\frac{3xy}{2}$是单项式 |
12．
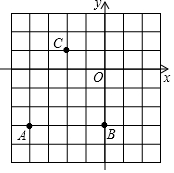已知：如图△ABC的顶点坐标分别为A（-4，-3），B（0，-3），C（-2，1），C点关于y轴对称的点为C′，若设△ABC的面积为S1，△ACC′的面积为S2，则S1，S2的大小关系为（ ）
已知：如图△ABC的顶点坐标分别为A（-4，-3），B（0，-3），C（-2，1），C点关于y轴对称的点为C′，若设△ABC的面积为S1，△ACC′的面积为S2，则S1，S2的大小关系为（ ）| A． | S1＞S2 | B． | S1=S2 | C． | S1＜S2 | D． | 不能确定 |
9．在平面直角坐标系中，第四象限的点是（ ）
| A． | （1，2） | B． | （-2，3） | C． | （-2，-3） | D． | （2，-3） |
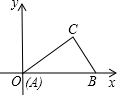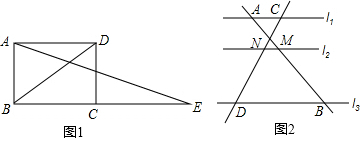
如图，Rt△ABC中，∠C=90°，AB=10，AC=8，Rt△ABC的斜边在x轴的正半轴上，点A与原点重合．随着顶点A由O点出发沿y轴的正半轴方向滑动，点B也沿着x轴向点O滑动，直到与点O重合时运动结束．在这个运动过程中．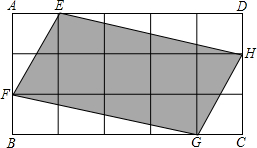
如图，将矩形ABCD分成15个大小相等的正方形，E、F、G、H分别在AD、AB、BC、CD边上，且是某个小正方形的顶点．若四边形EFGH的面积为1，则矩形ABCD的面积为$\frac{5}{3}$．