题目内容
 如图,在矩形ABCD中,点E为CD上一点,且AE=AB,连BE,求证:∠BAE=2∠CBE.
如图,在矩形ABCD中,点E为CD上一点,且AE=AB,连BE,求证:∠BAE=2∠CBE.考点:矩形的性质
专题:
分析:先根据矩形的性质得出∠ABC=90°,再根据直角三角形的两个锐角互余关系和等腰三角形的两个底角相等以及三角形内角和即可得出结论.
解答:
证明:∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠CBE+∠ABE=90°,
∵AE=AB,
∴∠ABE=∠AEB,
∵∠ABE+∠AEB+∠BAE=180°,
∴∠ABE+∠AEB+∠BAE=2(∠CBE+∠ABE),
∴∠BAE=2∠CBE.
∴∠ABC=90°,
∴∠CBE+∠ABE=90°,
∵AE=AB,
∴∠ABE=∠AEB,
∵∠ABE+∠AEB+∠BAE=180°,
∴∠ABE+∠AEB+∠BAE=2(∠CBE+∠ABE),
∴∠BAE=2∠CBE.
点评:本题考查了矩形的性质、直角三角形的性质、等腰三角形的性质以及三角形内角和;熟练掌握有关定理进行推理论证是解决问题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
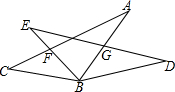 如图,BC=BE,∠C=∠E,∠CBE=∠ABD,则下列结论错误的是( )
如图,BC=BE,∠C=∠E,∠CBE=∠ABD,则下列结论错误的是( )| A、∠A=∠D |
| B、BF=BG |
| C、AC=DE |
| D、BA=BD |
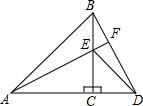 如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F.
如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F. 某班在一次测试中,一道计算题(满分5分)的得分情况如图.则这题得分的平均数是
某班在一次测试中,一道计算题(满分5分)的得分情况如图.则这题得分的平均数是
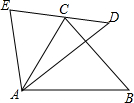 如图,E、C、D三点在一条直线上,AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.
如图,E、C、D三点在一条直线上,AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.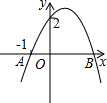 如图,二次函数y=ax2+bx+2的图象与x轴交于点A(-1,0)、B(x1,0),顶点在第一象限.下列结论:①ab<0;②0<b<2;③x1>2;④关于x的方程ax2+bx+1=0有两个不相等实数根;⑤将该抛物线沿某一方向平移后所得抛物线y=ax2+bx与x轴交于点C、D,则AB-CD=2.其中正确结论的个数为( )
如图,二次函数y=ax2+bx+2的图象与x轴交于点A(-1,0)、B(x1,0),顶点在第一象限.下列结论:①ab<0;②0<b<2;③x1>2;④关于x的方程ax2+bx+1=0有两个不相等实数根;⑤将该抛物线沿某一方向平移后所得抛物线y=ax2+bx与x轴交于点C、D,则AB-CD=2.其中正确结论的个数为( )
 如图,AB是⊙O的直径,C是⊙O上一点,若∠A=25°,则∠B=
如图,AB是⊙O的直径,C是⊙O上一点,若∠A=25°,则∠B=