题目内容
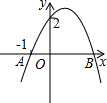 如图,二次函数y=ax2+bx+2的图象与x轴交于点A(-1,0)、B(x1,0),顶点在第一象限.下列结论:①ab<0;②0<b<2;③x1>2;④关于x的方程ax2+bx+1=0有两个不相等实数根;⑤将该抛物线沿某一方向平移后所得抛物线y=ax2+bx与x轴交于点C、D,则AB-CD=2.其中正确结论的个数为( )
如图,二次函数y=ax2+bx+2的图象与x轴交于点A(-1,0)、B(x1,0),顶点在第一象限.下列结论:①ab<0;②0<b<2;③x1>2;④关于x的方程ax2+bx+1=0有两个不相等实数根;⑤将该抛物线沿某一方向平移后所得抛物线y=ax2+bx与x轴交于点C、D,则AB-CD=2.其中正确结论的个数为( )| A、2个 | B、3个 | C、4个 | D、5个 |
考点:抛物线与x轴的交点,二次函数图象与系数的关系
专题:
分析:采用形数结合的方法解题,根据抛物线的开口方向,对称轴的位置判断a、b、c的符号,把两根关系与抛物线与x轴的交点情况结合起来分析问题.
解答:
 解:如图,对称轴在y轴的右侧,则a、b异号,即ab<0.故①正确;
解:如图,对称轴在y轴的右侧,则a、b异号,即ab<0.故①正确;
∵图象过A点,
∴a-b+2=0,解得a=b-2,且a<0,b>0,
∴b-2<0,可得0<b<2,
故②正确;
由根与系数的关系可得-1×x1=
=
,
∴x1=
,
∵0<b<2,
∴
>1,故③不正确;
令y=ax2+bx+1,则其图象相当于y=ax2+bx+2的图象向下平移一个单位,且最大值大于2,
∴y=ax2+bx+1的图象与x轴有两个交点,
∴方程ax2+bx+1=0有两个不相等的实数根,故④正确;
由题可知AB=x1+1=
+1=
,
在y=ax2+bx中,令y=0可得ax2+bx=0,可解得x=0或x=-
=
,
∴CD=
,
∴AB-CD=
-
=2,故⑤正确;
综上可知正确的为①②④⑤共4个,
故选C.
 解:如图,对称轴在y轴的右侧,则a、b异号,即ab<0.故①正确;
解:如图,对称轴在y轴的右侧,则a、b异号,即ab<0.故①正确;∵图象过A点,
∴a-b+2=0,解得a=b-2,且a<0,b>0,
∴b-2<0,可得0<b<2,
故②正确;
由根与系数的关系可得-1×x1=
| 2 |
| a |
| 2 |
| b-2 |
∴x1=
| 2 |
| 2-b |
∵0<b<2,
∴
| 2 |
| 2-b |
令y=ax2+bx+1,则其图象相当于y=ax2+bx+2的图象向下平移一个单位,且最大值大于2,
∴y=ax2+bx+1的图象与x轴有两个交点,
∴方程ax2+bx+1=0有两个不相等的实数根,故④正确;
由题可知AB=x1+1=
| 2 |
| 2-b |
| 4-b |
| 2-b |
在y=ax2+bx中,令y=0可得ax2+bx=0,可解得x=0或x=-
| b |
| a |
| b |
| 2-b |
∴CD=
| b |
| 2-b |
∴AB-CD=
| 4-b |
| 2-b |
| b |
| 2-b |
综上可知正确的为①②④⑤共4个,
故选C.
点评:主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,根的判别式的熟练运用.

练习册系列答案
相关题目
下列调查最适合用抽样调查的是( )
| A、某书稿中的错别字 |
| B、某品牌灯泡的使用寿命 |
| C、调查七(1)班学生的身高情况 |
| D、调查一个社区所有家庭的年收入 |
直角三角形的两条边分别是6和8,这第三条边的长度是( )
| A、6 | B、8 |
| C、10 | D、以上答案都不对 |
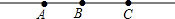 如图,下列说法错误的是( )
如图,下列说法错误的是( )| A、线段AB和线段BA是同一条线段 |
| B、直线AB和直线BA是同一条直线 |
| C、射线BC和射线CB是同一条射线 |
| D、射线AB和射线AC是同一条射线 |
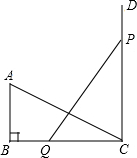 如图,△ABC中,∠B=90°,∠ACB=36°,AB=5,BC=10,CD⊥BC于点C,P、Q分别是CD、BC上的动点,PQ=AC.当∠QPC=
如图,△ABC中,∠B=90°,∠ACB=36°,AB=5,BC=10,CD⊥BC于点C,P、Q分别是CD、BC上的动点,PQ=AC.当∠QPC= 如图,在矩形ABCD中,点E为CD上一点,且AE=AB,连BE,求证:∠BAE=2∠CBE.
如图,在矩形ABCD中,点E为CD上一点,且AE=AB,连BE,求证:∠BAE=2∠CBE.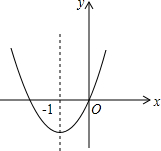 二次函数y=x2+bx的图象如图,对称轴为x=-1,若关于x的一元二次方程x2+bx-t=0(t为实数)在-4<x<1的范围内有解,则t的取值范围是
二次函数y=x2+bx的图象如图,对称轴为x=-1,若关于x的一元二次方程x2+bx-t=0(t为实数)在-4<x<1的范围内有解,则t的取值范围是