题目内容
7.在等边△ABC的外侧作直线BM,点A关于直线BM的对称点为D,连结AD,CD,设CD交直线BM于点E.
(1)依题意补全图1,若∠ABM=30°,求∠BCE的度数;
(2)如图2,若60°<∠ABM<90°,判断直线BM和CD相交所成的锐角的度数是否为定值?若是,求出这个锐角的度数;若不是,请说明理由.
分析 (1)根据题意可以作出相应的图形,连接BD,由题意可得到四边形ADBC是菱形,根据菱形的对角线平分每一组对角,可以得到∠BCE的度数;
(2)画出相应的图形,根据对称的性质可以得到相等的线段和相等的角,由等边△ABC,可以得到BC=BA,然后根据三角形内角和是180°,可以推出直线BM和CD相交所成的锐角的度数,本题得以解决.
解答 解:(1)补全的图1如下所示: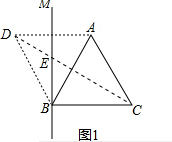
连接BD,如上图1所示,
∵由已知可得,BM垂直平分AD,∠ABM=30°,△ABC是等边三角形,
∴△BDA是等边三角形,AD∥BC且AD=BC,DA=DB,
∴四边形ADBC是菱形,
∵∠ACB=60°,
∴∠BCE=30°;
(2)直线BM和CD相交所成的锐角的度数是定值,若下图所示,
连接AE交BC于点F,
由已知可得,BD=BA,BA=BC,ED=EA,
则∠BDA=∠BAD,∠EDA=∠EAD,BD=BC,
∴∠BDC=∠BCD,∠EDB=∠EAB,
∴∠BCD=∠EAB,
∵∠EFC=∠BFA,∠ABC=60°,
∴∠CEA=∠ABC=60°,
∵∠AEC+∠AEM+∠DEM=180°,∠DEM=∠AEM,
∴∠DEM=60°,
即直线BM和CD相交所成的锐角的度数是定值,这个锐角的度数是60°.
点评 本题考查了根据轴对称变换作图以及等腰三角形的性质、等边三角形的性质、三角形的内角和、菱形的性质,解答本题的关键是明确题意,画出相应的图形,根据所求问题可以探索出所求问题需要的条件.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
15.甲队有工人96人,乙队有工人72人,如果要求乙队的人数是甲队人数的$\frac{1}{3}$,应从乙队调多少人去甲队,如果设应从乙队调x人到甲队,列出的方程正确的是( )
| A. | 96+x=$\frac{1}{3}$(72-x) | B. | $\frac{1}{3}$(96-x)=72-x | C. | $\frac{1}{3}$(96+x)=72-x | D. | $\frac{1}{3}$×96+x=72-x |
2. 如图,⊙O是△ABC的外接圆,连接OA、OB,∠AOB=50°,则∠C的度数为( )
如图,⊙O是△ABC的外接圆,连接OA、OB,∠AOB=50°,则∠C的度数为( )
 如图,⊙O是△ABC的外接圆,连接OA、OB,∠AOB=50°,则∠C的度数为( )
如图,⊙O是△ABC的外接圆,连接OA、OB,∠AOB=50°,则∠C的度数为( )| A. | 25° | B. | 40° | C. | 50° | D. | 80° |
 如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x.
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x. 用4个棱长为1的正方体搭成一个几何模型,其从正面、左面看到的图形如图所示,则该几何体从上面看到的图形不可能为( )
用4个棱长为1的正方体搭成一个几何模型,其从正面、左面看到的图形如图所示,则该几何体从上面看到的图形不可能为( )



 如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为A、B.
如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为A、B. 如图,∠AOB=42°,∠BOC=86°,OD为∠AOC的平分线,∠BOD=22°.
如图,∠AOB=42°,∠BOC=86°,OD为∠AOC的平分线,∠BOD=22°. 已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过5次翻转之后,点B的坐标是(11,$\sqrt{3}$).
已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过5次翻转之后,点B的坐标是(11,$\sqrt{3}$). 如图,直线AB,CD,EF相交于点O,且∠AOD=90°,∠1=40°,求∠2的度数.
如图,直线AB,CD,EF相交于点O,且∠AOD=90°,∠1=40°,求∠2的度数.