题目内容
4.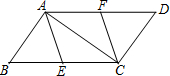 已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF.
已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF.(1)四边形AECF是什么特殊四边形?证明你的结论;
(2)当△ABC的角满足什么条件时,四边形AECF是正方形?证明你的结论.
分析 (1)平行四边形的性质得出AD=BC,AD∥BC,求出AF=CE,AF∥CE,求出四边形AECF是平行四边形,求出∠AEC=90°,即可得出答案;
(2)求出AE=EC=$\frac{1}{2}$BC,即可得出答案.
解答 (1)四边形AECF是矩形,
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵E、F分别是BC、AD的中点,
∴AF=$\frac{1}{2}$AD,CE=$\frac{1}{2}$BC,
∴AF=CE,AF∥CE,
∴四边形AECF是平行四边形,
∵AB=AC,E为BC的中点,
∴AE⊥BC,
∴∠AEC=90°,
∴四边形AECF是矩形;
(2)当△ABC满足∠BAC=90°时,四边形AECF是正方形,
证明:∵∠BAC=90°,E为BC的中点,
∴AE=EC=$\frac{1}{2}$BC,
∵四边形AECF是矩形,
∴四边形AECF是正方形,
∴当△ABC满足∠BAC=90°时,四边形AECF是正方形.
点评 本题考查了矩形的判定、菱形的判定、正方形的判定,平行四边形的性质和判定,等腰三角形的性质,直角三角形的性质的应用,能综合运用知识点进行推理是解此题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
15.甲队有工人96人,乙队有工人72人,如果要求乙队的人数是甲队人数的$\frac{1}{3}$,应从乙队调多少人去甲队,如果设应从乙队调x人到甲队,列出的方程正确的是( )
| A. | 96+x=$\frac{1}{3}$(72-x) | B. | $\frac{1}{3}$(96-x)=72-x | C. | $\frac{1}{3}$(96+x)=72-x | D. | $\frac{1}{3}$×96+x=72-x |
9. 如图,正方体表面上画有一条黑色线条,则其俯视图是( )
如图,正方体表面上画有一条黑色线条,则其俯视图是( )
 如图,正方体表面上画有一条黑色线条,则其俯视图是( )
如图,正方体表面上画有一条黑色线条,则其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,小亮以0.5m/s的速度从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,从开始到停止共所需时间为480s.
如图,小亮以0.5m/s的速度从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,从开始到停止共所需时间为480s. 如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为A、B.
如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为A、B. 如图,∠AOB=42°,∠BOC=86°,OD为∠AOC的平分线,∠BOD=22°.
如图,∠AOB=42°,∠BOC=86°,OD为∠AOC的平分线,∠BOD=22°. 已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过5次翻转之后,点B的坐标是(11,$\sqrt{3}$).
已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过5次翻转之后,点B的坐标是(11,$\sqrt{3}$). 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是直线x=2,与x轴的一个交点是(-1,0),有下列结论:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是直线x=2,与x轴的一个交点是(-1,0),有下列结论: