题目内容
14.(1)先化简,再求值:(1-$\frac{1}{a-2}$)÷$\frac{a-2}{{a}^{2}-4}$,其中a=-3.(2)解方程:$\frac{x}{x-1}$+$\frac{2}{1-x}$=2.
分析 (1)先化简分式,再进一步代入求得答案即可;
(2)利用解分式方程的步骤与方法求得未知数的值即可.
解答 解:(1)原式=$\frac{a-3}{a-2}$•$\frac{(a+2)(a-2)}{a-2}$
=$\frac{(a-3)(a+2)}{a-2}$
当a=-3时,
原式=-$\frac{6}{5}$.
(2)$\frac{x}{x-1}$+$\frac{2}{1-x}$=2
方程两边同乘(x-1)得,x-2=2(x-1)
解得:x=0
检验:当x=0时,x-1≠0,
所以x=0是原分式方程的解.
点评 此题考查分式的化简求值与解分式方程,掌握化简方法与解方程的步骤与方法是解决问题的关键.

练习册系列答案
相关题目
2.已知函数y=-x2+2x-2-c2(c为常数)的图象上有两点A(x1,y1),B(x2,y2),若x1<1<x2且x1+x2>2,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1与y2的大小不确定 |
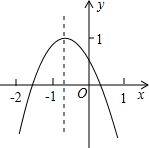 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )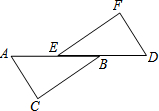 如图,A,E,B,D在同一直线上,在△ABC与△DEF中,AB=DE,AC=DF,AC∥DF.求证:∠C=∠F.
如图,A,E,B,D在同一直线上,在△ABC与△DEF中,AB=DE,AC=DF,AC∥DF.求证:∠C=∠F.