题目内容
8.在△ABC中,若${(sinA-\frac{{\sqrt{3}}}{2})^2}$+|tanB-1|=0,则∠C=75°.分析 根据非负数的性质分别求出∠A,∠B的度数即可解决问题.
解答 解:∵${(sinA-\frac{{\sqrt{3}}}{2})^2}$+|tanB-1|=0,
又∵${(sinA-\frac{{\sqrt{3}}}{2})^2}$≥0,|tanB-1|≥0,
∴sinA=$\frac{\sqrt{3}}{2}$,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°-∠A-∠B=75°.
故答案为75°.
点评 本题考查非负数的性质、三角函数等知识,解题的关键是连接非负数的性质,记住特殊角的三角函数值,属于中考常考题型.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
16.若$\sqrt{40.40}$=6.356,则$\sqrt{0.404}$=( )
| A. | 63.56 | B. | 0.006356 | C. | 635.6 | D. | 0.6356 |
13.下列说法正确的是( )
| A. | 一个有理数的平方根有两个,它们互为相反数 | |
| B. | 一个有理数的立方根,不是正数就是负数 | |
| C. | 负数没有立方根 | |
| D. | 如果一个数的立方根等于这个数的算术平方根,则这个数一定是0或1 |
17.方程2x2-5x+3=0的根的情况是( )
| A. | 有一个实数根 | B. | 没有实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
18.下列小数可用科学记数法表示为8.02×10-5的是( )
| A. | 0.00000802 | B. | 0.0000802 | C. | 0.00802 | D. | 802000 |
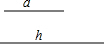 如图,已知两条线段的长度分别为a和h.
如图,已知两条线段的长度分别为a和h.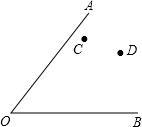 如图所示,点C、D是∠AOB内部的两点.
如图所示,点C、D是∠AOB内部的两点.