题目内容
19.求使下列各式有意义的x的取值范围:(1)$\sqrt{5-2x}$;(2)$\sqrt{{x}^{2}+5}$;(3)$\sqrt{-\frac{x}{2}+1}$.分析 根据二次根式的性质,被开方数大于等于0可知.
解答 解:(1)根据题意,得:5-2x≥0,解得:x≤$\frac{5}{2}$,
即x≤$\frac{5}{2}$时,$\sqrt{5-2x}$有意义;
(2)依题意有x2+5>0,故x取全体实数,$\sqrt{{x}^{2}+5}$都有意义;
(3)根据题意,-$\frac{x}{2}$+1≥0,解得:x≤2,
即x≤2时,$\sqrt{-\frac{x}{2}+1}$有意义.
点评 主要考查了二次根式的意义和性质.概念:式子$\sqrt{a}$(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.

练习册系列答案
相关题目
15.“十一”黄金周期间,某动物园在7天假期中每天旅游的人数变化如表:(正数表示比前一天多的人数,负数表示比前一天少的人数).
(1)若9月30日的游客人数记为a万人,则10月1日的游客人数为:(a+1.6)万人.(请用含a的代数式表示)
(2)请问七天内游客人数最多的是哪天?最少的是哪天?(请说明理由)
(3)若9月30日的游客人数为2万人,门票为每人10元,则黄金周期间该动物园门票收入是多少万元?
| 日期(10月) | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请问七天内游客人数最多的是哪天?最少的是哪天?(请说明理由)
(3)若9月30日的游客人数为2万人,门票为每人10元,则黄金周期间该动物园门票收入是多少万元?
7.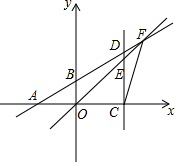 如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.
如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.
 如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.
如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
4.下列结论正确的是( )
| A. | 2-1=-2 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x-2}$有意义的x的取值范围是x<2 | |
| D. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=-1 |
9.下列计算正确的是( )
| A. | (x4)4=x8 | B. | (mn)2(-m4)=-m6n2 | C. | a2•a3=a6 | D. | 2x(-3xy)2=-6x3y2 |
 如图,已知∠α,利用尺规求作一个∠AOB,使得∠AOB=2∠α(不写作法,保留作图痕迹)
如图,已知∠α,利用尺规求作一个∠AOB,使得∠AOB=2∠α(不写作法,保留作图痕迹)