题目内容

17．方程2x2-5x+3=0的根的情况是（　　）
A．有一个实数根B．没有实数根
C．有两个相等的实数根D．有两个不相等的实数根

分析 把a=2，b=-5，c=3代入△=b2-4ac进行计算，然后根据计算结果判断方程根的情况．

解答 解：∵a=2，b=-5，c=3，
∴△=b2-4ac=（-5）2-4×2×3=1＞0，
∴方程有两个不相等的实数根．
故选D．

点评 本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的判别式△=b2-4ac．当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程没有实数根．

练习册系列答案
相关题目
7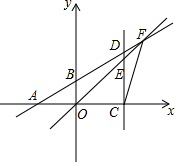．如图，点A、B坐标分别为A（-2，0），B（0，1），点E是坐标平面内的任意一点，过点E作x轴的垂线交x轴于点C，交直线AB于点D，直线OE交直线AB于点F，连接CF，若△CEF是一个有一内角为120°的等腰三角形，则符合条件的点E的有（　　）个．
A．3个B．4个C．5个D．6个
8．在△ABC中，若${（sinA-\frac{{\sqrt{3}}}{2}）^2}$+|tanB-1|=0，则∠C=75°．
5．下列说法不正确的是（　　）
A．两个单项式的积仍然是单项式
B．两个非零单项式的积的次数等于它们的次数的和
C．不为零的单项式乘以多项式，积的项数与多项式项数相同
D．多项式乘以多项式，合并同类项前，积的项数等于两个多项式的项数的和
12．下列式子中正确的是（　　）
A．$\sqrt{-5}=-\sqrt{5}$B．$\root{3}{-8}$=-2C．$\sqrt{16}=±4$D．-$\sqrt{（-\frac{1}{2}）^{2}}$=$\frac{1}{2}$
2．下列各式中正确的是（　　）
A．$\sqrt{25}$=±5B．$\sqrt{-16}$=4C．$\sqrt{2\frac{1}{4}}$=$\frac{3}{4}$D．$\sqrt{9}$=3
9．下列计算正确的是（　　）
A．（x4）4=x8B．（mn）2（-m4）=-m6n2C．a2•a3=a6D．2x（-3xy）2=-6x3y2
6．下列整式运算正确的是（　　）
A．2x2-3x2=x2B．2x3•3x2-3x2•2x3=-x5
C．2（-x）6÷（-$\frac{1}{2}$x2）=4x4D．（2x2）3+2x6=10x6
7．若16x2+mxy+25y2是一个完全平方式，那么m的值是（　　）
A．20B．±20C．40D．±40

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网