题目内容
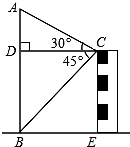 如图,在数学活动课中,小张为了测量校园内旗杆AB的高度,站在教学楼的顶端C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°,已知旗杆与教学楼的水平距离CD为10m.
如图,在数学活动课中,小张为了测量校园内旗杆AB的高度,站在教学楼的顶端C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°,已知旗杆与教学楼的水平距离CD为10m.(1)直接写出教学楼CE的高度;
(2)求旗杆AB的高度.(结果保留根号)
考点:解直角三角形的应用-仰角俯角问题
专题:应用题
分析:(1)CE=BD=CD,继而可得出CE的高度.
(2)在Rt△ACD中求出AD的长度,继而可得AB的高度.
(2)在Rt△ACD中求出AD的长度,继而可得AB的高度.
解答:解:(1)CE=10(m);
(2)在Rt△ACD中,
∵tan∠ACD=
,
∴AD=CD•tan∠ACD=10•tan30°=
(m),
∴AB=AD+BD=
(m).
答:旗杆的高度是
m.
(2)在Rt△ACD中,
∵tan∠ACD=
| AD |
| CD |
∴AD=CD•tan∠ACD=10•tan30°=
10
| ||
| 3 |
∴AB=AD+BD=
10
| ||
| 3 |
答:旗杆的高度是
10
| ||
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是熟练掌握锐角三角函数的定义,能运用锐角三角函数及已知线段表示出未知线段的长度.

练习册系列答案
相关题目
 如图,在?ABCD中,E、F为对角线BD上的两点,且BE=DF.求证:∠BAE=∠DCF.
如图,在?ABCD中,E、F为对角线BD上的两点,且BE=DF.求证:∠BAE=∠DCF.