题目内容
某超市经营甲、乙两种商品,甲每件进价10元,售价15元;乙每件进价15元,售价25元;元旦前夕,超市购进甲、乙两种商品共90件,总进价恰好为1100元;
(1)求超市购进甲、乙两种商品各多少件?
(2)超市把甲商品的售价提高20%,乙商品按售价打折销售,将这些商品全部售完后可获利500元,那么超市将乙商品打几折售出?
(3)在元旦当天,该超市对甲、乙两种商品进行如下的优惠促销活动:
按上述优惠条件,若小明买这两种商品共付款315元,小华购买乙种商品共付款432元;如果你替他们一次性够买这些商品可以省多少钱?
(1)求超市购进甲、乙两种商品各多少件?
(2)超市把甲商品的售价提高20%,乙商品按售价打折销售,将这些商品全部售完后可获利500元,那么超市将乙商品打几折售出?
(3)在元旦当天,该超市对甲、乙两种商品进行如下的优惠促销活动:
| 商品价格 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元,但不超过500元 | 全部打九折 |
| 超过500元 | 全部打八折 |
考点:一元一次方程的应用
专题:
分析:(1)设购进甲商品x件,则购进乙商品(90-x)件,根据总进价恰好为1100元列方程10x+15(90-x)=1100,再解方程求出x,然后计算90-x;
(2)设乙商品打x折出售,甲商品每件获利(1.2×15-10),乙商品每件获利(25×0.1x-15),然后根据总利润解方程(1.2×15-10)×50+(25×0.1x-15)×40=500,再解一次方程即可;
(3)先按打九折计算小明所购商品的价格为350,再按打九折或八折计算小华购买的商品的价格为480或540,然后计算若一次性付款打八折所需费用,再计算两者的差即可.
(2)设乙商品打x折出售,甲商品每件获利(1.2×15-10),乙商品每件获利(25×0.1x-15),然后根据总利润解方程(1.2×15-10)×50+(25×0.1x-15)×40=500,再解一次方程即可;
(3)先按打九折计算小明所购商品的价格为350,再按打九折或八折计算小华购买的商品的价格为480或540,然后计算若一次性付款打八折所需费用,再计算两者的差即可.
解答:解:(1)设购进甲商品x件,则购进乙商品(90-x)件,
依题意得:10x+15(90-x)=1100,解得 x=50,
所以90-x=40.
答:购进甲商品50件,购进乙商品40件;
(2)设乙商品打x折出售,
依题意得:(1.2×15-10)×50+(25×0.1x-15)×40=500
解得x=7.
答:乙商品打7折售出;
(3)小明所购商品的价格为:315÷0.9=350,
小华购买的商品的价格为:432÷0.9=480或432÷0.8=540,
若一次性付款为:(350+480)×0.8=664 或(350+540)×0.8=712,
则可省:315+432-664=83或315+432-712=35
答:可省83元或35元.
依题意得:10x+15(90-x)=1100,解得 x=50,
所以90-x=40.
答:购进甲商品50件,购进乙商品40件;
(2)设乙商品打x折出售,
依题意得:(1.2×15-10)×50+(25×0.1x-15)×40=500
解得x=7.
答:乙商品打7折售出;
(3)小明所购商品的价格为:315÷0.9=350,
小华购买的商品的价格为:432÷0.9=480或432÷0.8=540,
若一次性付款为:(350+480)×0.8=664 或(350+540)×0.8=712,
则可省:315+432-664=83或315+432-712=35
答:可省83元或35元.
点评:本题考查了一元一次方程的应用:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
若一个多边形的内角和等于1080°,则这个多边形的边数是( )
| A、9 | B、8 | C、7 | D、6 |
与代数式1-y+y2-y3相等的式子是( )
| A、1-(y+y2-y3) |
| B、1-(y-y2-y3) |
| C、1-(y-y2+y3) |
| D、1-(-y+y2-y3) |

 如图,在平面直角坐标系中,△ABC与△A′B′C′关于点P位似,且顶点都在格点上.
如图,在平面直角坐标系中,△ABC与△A′B′C′关于点P位似,且顶点都在格点上. 已知:如图,△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,点E是BC上一点,且BD=BE.求∠DEC的度数.
已知:如图,△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,点E是BC上一点,且BD=BE.求∠DEC的度数.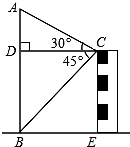 如图,在数学活动课中,小张为了测量校园内旗杆AB的高度,站在教学楼的顶端C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°,已知旗杆与教学楼的水平距离CD为10m.
如图,在数学活动课中,小张为了测量校园内旗杆AB的高度,站在教学楼的顶端C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°,已知旗杆与教学楼的水平距离CD为10m. 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.
如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.