题目内容
5.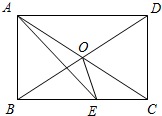 如图,矩形ABCD中,对角线AC、BD交于点O,在BC上取BE=BO,连结AE,且∠BOE=75°.
如图,矩形ABCD中,对角线AC、BD交于点O,在BC上取BE=BO,连结AE,且∠BOE=75°.(1)求∠ABO的度数;
(2)求∠CAE的度数.
分析 (1)根据等腰三角形的性质求出∠OBE=30°,则求该角的余角即可;
(2)根据矩形的对角线互相平分且相等可得OA=OB,然后求出△AOB是等边三角形,根据等边三角形的性质可得AB=BO,∠BAO=60°,再判断出△ABE是等腰直角三角形,根据等腰直角三角形的性质求出∠BAE=45°,然后根据∠CAE=∠BAO-∠BAE计算即可得解.
解答 解:(1)解:∵BE=BO,∠BOE=75°,
∴∠OBE=180°-2×75°=30°,
∴∠ABO=∠ABC-∠OBE=90°-30°=60°;
(2)由(1)知,∠ABO=60°.
∵四边形ABCD是矩形,
∴OA=OB,
∴△AOB是等边三角形,
∴AB=BO,∠BAO=60°,
∵BO=BE,
∴AB=BE,
∴△ABE是等腰直角三角形,
∴∠BAE=45°,
∴∠CAE=∠BAO-∠BAE=60°-45°=15°.
点评 本题考查了矩形的性质,等腰三角形的性质,等边三角形的判定与性质,等腰直角三角形的判定与性质,熟记各性质并判断出等边三角形和等腰直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.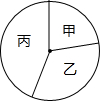 如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
 如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )| A. | $\frac{2}{3}$π | B. | $\frac{4}{9}$π | C. | 3π | D. | 4π |
 如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.
如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC. 如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.
如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.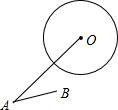 如图,⊙O的半径为1,OA=2.5,∠OAB=30°,则AB与⊙O的位置关系是相离.
如图,⊙O的半径为1,OA=2.5,∠OAB=30°,则AB与⊙O的位置关系是相离.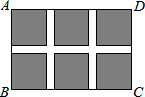 如图,某小区规划在一个长30m、宽20m的长方形ABCD土地上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程x2-35x+66=0.
如图,某小区规划在一个长30m、宽20m的长方形ABCD土地上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程x2-35x+66=0.