题目内容
3.若(a+1)x|a|+3y=1是关于x、y的二元一次方程,则a=1.分析 根据二元一次方程的定义求解即可.
解答 解:由(a+1)x|a|+3y=1是关于x、y的二元一次方程,
得|a|=1且a+1≠0,
解得a=1.
故答案为:1.
点评 本题考查了二元一次方程,二元一次方程必须符合以下三个条件:(1)方程中只含有2个未知数;(2)含未知数项的最高次数为一次;(3)方程是整式方程.

练习册系列答案
相关题目
11.如图,将一个长为12cm,宽为6cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )


| A. | 9cm2 | B. | 18cm2 | C. | 27cm2 | D. | 72cm2 |
8.问题提出:用水平线和竖直线将平面分成若干个面积为1的小长方形格子,小长方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x,多边形内部的格点数为n,S与x,n之间是否存在一定的数量关系呢?
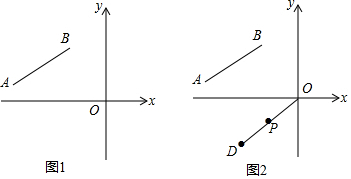
问题探究:(1)如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S=$\frac{1}{2}$x.
(2)在图2中所示的格点多边形,这些多边形内部都有且只有2个格点.探究此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=$\frac{1}{2}$x+1.
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=$\frac{1}{2}$x+(n-1)(用含有字母x,n的代数式表示)
问题拓展:请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:
则S与a,b之间的关系为S=a+2b-2(用含a,b的代数式表示).

问题探究:(1)如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S=$\frac{1}{2}$x.
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=$\frac{1}{2}$x+(n-1)(用含有字母x,n的代数式表示)
问题拓展:请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:
| 格点多边形各边上的格点的个数 | 格点多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1(图3) | 8 | 1 | 8 |
| 多边形2(图4) | 7 | 3 | 11 |
| … | … | … | … |
| … | … | … | … |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
15.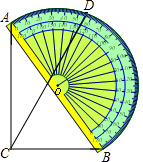 如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
 如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )| A. | 63° | B. | 54° | C. | 36° | D. | 27° |
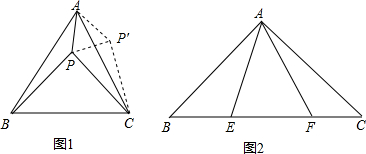
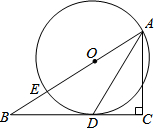 如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.