题目内容
10.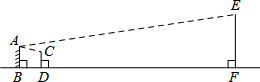 如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为7m.
如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为7m.
分析 过C′作C′H∥FD分别交AB、CD于G、H,根据EF∥AB∥C′D′可求出AG、EG、GH,再根据相似三角形的判定定理可得△C′AG∽△C′EH,再根据三角形的相似比解答即可.
解答 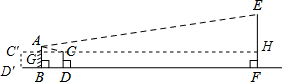 解:过C′作C′H∥FD分别交AB、CD于G、H.
解:过C′作C′H∥FD分别交AB、CD于G、H.
因为EF∥AB∥C′D′,所以HF=GB=C′D′.
所以AG=AB-GB=AB-C′D′=2-1.5=0.5m
C′G=D′B=2m,GH=BF=20m
CH=CD-1.5m
又因为$\frac{EH}{AG}$=$\frac{C′H}{C′G}$,
所以$\frac{EH}{0.5}$,
所以EH=5.5m,
即旗杆的高EF=7m.
故答案为:7m.
点评 本题考查了相似三角形的应用,此题难度不大,解答此题的关键是作出辅助线.构造出相似三角形,利用平行线的性质及相似三角形的相似比解答.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
20.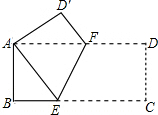 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )
如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )
 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )
如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )| A. | 4$\sqrt{5}$ | B. | 8 | C. | 6 | D. | 10 |
2.下列说法错误的是( )
| A. | 4的算术平方根是2 | B. | $\sqrt{81}$的平方根是±3 | ||
| C. | 8的立方根是±2 | D. | 0的平方根是0 |
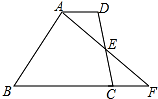 如图,在四边形ABCD中,AD∥BC,E为CD中点,连接AE并延长交BC的延长线于点F.
如图,在四边形ABCD中,AD∥BC,E为CD中点,连接AE并延长交BC的延长线于点F.